题目内容
(本题满分14分)
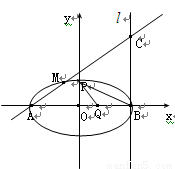
(文)如图,|AB|=2,O为AB中点,直线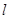 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与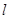 交于点C,点M在线段AC上,满足
交于点C,点M在线段AC上,满足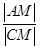 =
=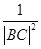 .
.
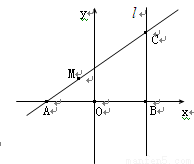
(I)求点M的轨迹方程;
(II)若过B点且斜率为- 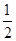 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为锐角三角形时t的取值范围.
【答案】
(1) x2+4y2=1(y≠0); (2) - 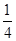 <t<0。
<t<0。
【解析】(1)设M(x,y),C(1,y0),然后再此条件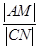 =
=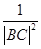 坐标化可得
坐标化可得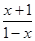 =
=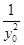 ,
,
再根据A、M、C三点一线,∴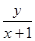 =
=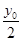 ,然后两式联立消去y0,即可得到点M的轨迹方程.要注意
,然后两式联立消去y0,即可得到点M的轨迹方程.要注意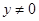 .
.
(2)用向量判定是锐角的条件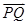 ·
·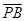 >0,并且
>0,并且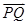 和
和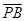 不共线,然后用坐标表示出来,即可得到t的取值范围.
不共线,然后用坐标表示出来,即可得到t的取值范围.
(1)设M(x,y),C(1,y0),∵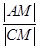 =
=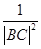 ,∴
,∴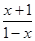 =
=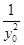 (2’)
(2’)
又A、M、C三点一线,∴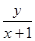 =
=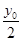 ②
(4’)
②
(4’)
由(1)、(2)消去y0,得x2+4y2=1(y≠0) (6’)
(2)P(0, 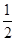 )是轨迹M短轴端点,∴t≥0时∠PQB或∠PBQ不为锐角,∴t<0
)是轨迹M短轴端点,∴t≥0时∠PQB或∠PBQ不为锐角,∴t<0
又∠QPB为锐角,∴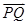 ·
·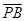 >0,∴(t,-
>0,∴(t,- 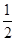 )(1,-
)(1,-
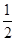 )=t+
)=t+
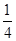 >0,∴-
>0,∴- 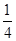 <t<0
(12’)
<t<0
(12’)

练习册系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).