题目内容
下图a是某市参加2012年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A1、A2、…、Am [如A2表示身高（单位：cm）在[150，155]内的学生人数]。图b是统计图a中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160～180cm（含160cm，不含180cm）的学生人数，那么在流程图中的判断框内应填写的条件是 （ ）
A． <9 | B．<8 | C．<7 | D．<6 |
B
解析试题分析：统计身高在160～180cm（含160cm，不含180cm）的学生人数即统计第4,5,6,7组的人数，而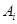
表示第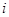
组的人数，所以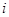的最大值为7，因此B正确
考点：程序框图
点评：程序框图题目关键是分析清楚程序循环的次数
练习册系列答案
相关题目
越大，说明残差平方和越小，模型的拟合效果越好；
一定过样本点的中心：（
；
中的
的值越大，说明“两个分类变量有关系”的可能性越强.两个变量有线性相关关系且正相关，则回归直线方程中，
的系数
（ ）
A． | B． | C． | D． |
在某次测量中得到的A样本数据如下：82,84,84,86,86,86,88,88,88,88.若B样本数据 恰好是A样本数据都加2后所得数据，则A，B两样本的下列数字特征对应相同的是
| A．众数 | B．平均数 | C．中位数 | D．标准差 |
变量x，y有观测数据(xi，yi)(i＝1,2，，10)，得散点图(1)；对变量u，v有观测数据( ui，
vi)(i ＝1,2，，10)，得散点图(2)．由这两个散点图可以判断．
| A．变量x与y正相关，u与v正相关 |
| B．变量x与y正相关，u与v负相关 |
| C．变量x与y负相关，u与v正相关 |
| D．变量x与y负相关，u与v负相关 |
在两个变量y与x的回归模型中，分别选择了4个不同模型，它们的
如下，其中拟合效果最好的模型是（ ）
| A．模型1的为0.975 | B．模型2的为0.79 |
| C．模型3的为0.55 | D．模型4的为0.25 |
某班50名学生其中考试数学成绩的频率分布直方图如图所示.其中成绩分组区间是：
，
， 
，
，
.则图中
的值为（ ）
| A．0.18 | B．0.018 | C．0.36 | D．0.009 |
一个样本a,3,5,7的平均数是b，且a、b是方程x2－5x＋4＝0的两根，则这个样本的方差是( )
| A．3 | B．4 | C．5 | D．6 |