题目内容
某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名。现用分层抽样的方法在这70名学生中抽样,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
| A.6 | B.10 | C. 8 | D.9 |
C
解析试题分析:分层抽样即按各层个体总数与样本容量的比例关系依次抽取各层个体的抽样方法。高一30名抽取了6名,抽取比例为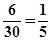 ,所以高二抽取的学生数为
,所以高二抽取的学生数为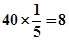 名
名
考点:分层抽样
点评:当抽取的对象差异较大时适宜采用分层抽样,容易题

练习册系列答案
相关题目
已知统计某产品的广告费用 (万元)与销售额
(万元)与销售额 (万元)所得的数据如下表所示:
(万元)所得的数据如下表所示:
 | 0 | 1 | 3 | 4 |
 | 2.2 | 4.3 | 4.8 | 6.7 |
 与
与 有较强的线性相关性,且
有较强的线性相关性,且 ,则
,则 等于
等于A. 2.6万元 B. 2.4万元 C. 2.7万元 D. 2.5万元
上海世博会期间,某日13时至21时累计入园人数的折线图如图所示,那么在13时~14时,14时~15时,……,20时~21时八个时段中,入园人数最多的时段是( )
| A.13时~14时 | B.16时~ 17时 | C. 18时~19时 | D. 19时~20时 |
一组数据中,每一个数都减去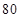 ,得到一组新数据,若求得新数据的平均数是
,得到一组新数据,若求得新数据的平均数是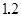 ,方差是
,方差是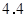 ,则原来数据的平均数和方差分别为( )
,则原来数据的平均数和方差分别为( )
A.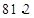 , , 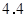 | B.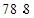 , , 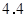 | C.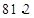 , , 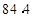 | D.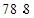 , ,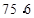 |
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长立形的面积等于其他10个小长方形的面积的和的 ,且样本容量为160,则中间一组数的频数为( )
,且样本容量为160,则中间一组数的频数为( )
| A.32 | B.0.2 | C.40 | D.0.25 |
某商场在国庆黄金周的促销活动中,对10月2日9时至14时的销售额进行统计,其频率分布直方图如图1所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为( )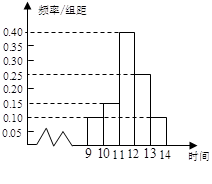
| A.6万元 | B.8万元 | C.10万元 | D.12万元 |
某个小区住户共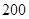 户,为调查小区居民的
户,为调查小区居民的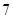 月份用水量,用分层抽样的方法抽取了
月份用水量,用分层抽样的方法抽取了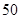 户进行调查,得到本月的用水量(单位:m3)的频率分布直方图如图所示,则小区内用水量超过
户进行调查,得到本月的用水量(单位:m3)的频率分布直方图如图所示,则小区内用水量超过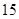 m3的住户的户数为( )
m3的住户的户数为( )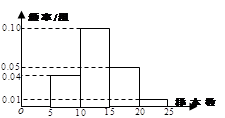
A.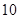 | B.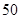 | C.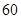 | D.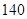 |
已知一组数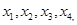 的平均数是
的平均数是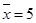 ,方差
,方差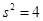 ,则数据
,则数据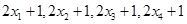 的平均数和方差分别是( )
的平均数和方差分别是( )
| A.11,8 | B.10,8 | C.11,16 | D.10,16 |

 <9
<9