题目内容
(本小题满分14分)
记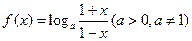 ,
,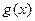 是
是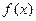 的反函数,
的反函数,
(Ⅰ)若关于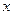 的方程:
的方程: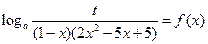 在
在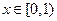 上有实数解,求实数
上有实数解,求实数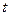 的取值范围。
的取值范围。
(Ⅱ)当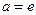 (
(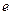 是自然对数的底数)时,记:
是自然对数的底数)时,记: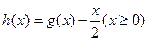 ,求函数
,求函数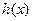 的最大值。
的最大值。
(Ⅲ)当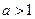 时,求证:
时,求证: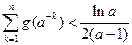 (
(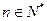 )
)
记
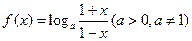 ,
,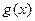 是
是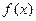 的反函数,
的反函数,(Ⅰ)若关于
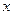 的方程:
的方程: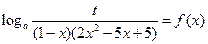 在
在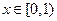 上有实数解,求实数
上有实数解,求实数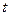 的取值范围。
的取值范围。(Ⅱ)当
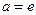 (
(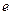 是自然对数的底数)时,记:
是自然对数的底数)时,记: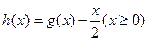 ,求函数
,求函数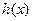 的最大值。
的最大值。(Ⅲ)当
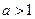 时,求证:
时,求证: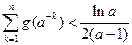 (
(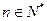 )
)1.条件可知: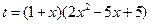 ,在
,在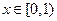 上有解。
上有解。
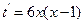 ,当
,当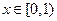 时,
时,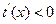 ,所以
,所以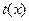 在
在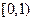 上单调递减。
上单调递减。
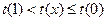 ,即
,即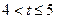 。 4分
。 4分
2.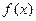 的定义域为(-1,1),
的定义域为(-1,1),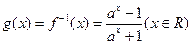
当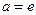 时,
时,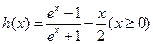 ,所以
,所以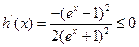 ,
,
所以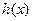 在
在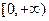 上单调递减。所以,
上单调递减。所以,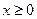 时,
时,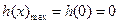 9分
9分
3.由2的启示可以设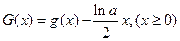
则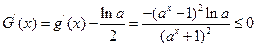 ,
,
所以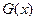 在
在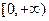 上单调递减,
上单调递减,
当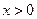 时,
时,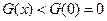 。即
。即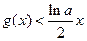
所以: 14分
14分
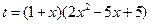 ,在
,在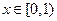 上有解。
上有解。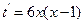 ,当
,当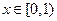 时,
时,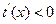 ,所以
,所以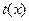 在
在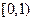 上单调递减。
上单调递减。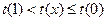 ,即
,即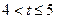 。 4分
。 4分2.
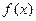 的定义域为(-1,1),
的定义域为(-1,1),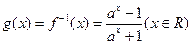
当
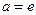 时,
时,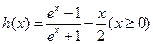 ,所以
,所以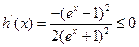 ,
,所以
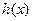 在
在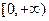 上单调递减。所以,
上单调递减。所以,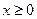 时,
时,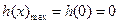 9分
9分3.由2的启示可以设
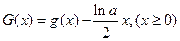
则
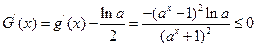 ,
,所以
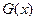 在
在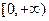 上单调递减,
上单调递减,当
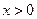 时,
时,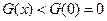 。即
。即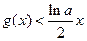
所以:
 14分
14分略

练习册系列答案
相关题目
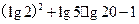


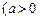 且
且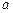 ≠1)
≠1)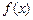 的单调性。(12分)
的单调性。(12分)
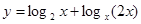 的值域是
的值域是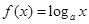 ,
,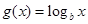 ,
,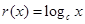 ,
, 的图象如图
的图象如图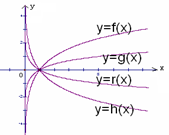





 则
则 =________
=________ ______.
______.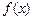 的图象与函数
的图象与函数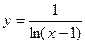 的图象关于直线
的图象关于直线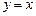 对称,则
对称,则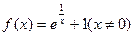
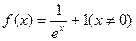
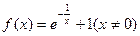
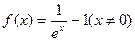





 (
(  )
)

