题目内容
已知实数 ,函数
,函数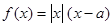 .
.
(I)讨论 在
在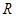 上的奇偶性;
上的奇偶性;
(II)求函数 的单调区间;
的单调区间;
(III)求函数 在闭区间
在闭区间 上的最大值。
上的最大值。
(I)当 时,
时,  为奇函数;当
为奇函数;当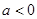 时,
时, 为非奇非偶函数;
为非奇非偶函数;
(II)函数 的增区间
的增区间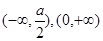 ,函数
,函数 的减区间
的减区间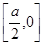 ;
;
(III)当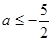 时,
时,  的最大值是
的最大值是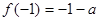
当 时,
时, 的最大值是
的最大值是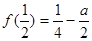 。
。
解析试题分析:(I)当 时,
时, 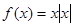 ,因为
,因为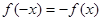 ,故
,故 为奇函数;
为奇函数;
当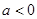 时,
时, 为非奇非偶函数 2分
为非奇非偶函数 2分
(II)当 时,
时,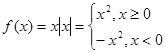 故函数
故函数 的增区间
的增区间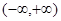 3分
3分
当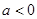 时,
时,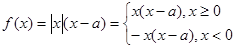
故函数 的增区间
的增区间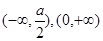 ,函数
,函数 的减区间
的减区间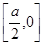 5分
5分
(III)①当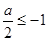 即
即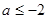 时,
时,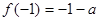 ,
,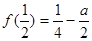
当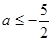 时,
时,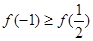 ,
, 的最大值是
的最大值是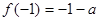
当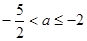 时,
时,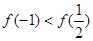 ,
, 的最大值是
的最大值是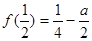 7分
7分
② 当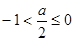 即
即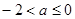 时,
时,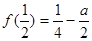 ,
,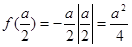 ,
,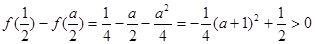 ,
,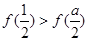
所以,当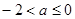 时,
时, 的最大值是
的最大值是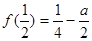 9分
9分
综上,当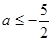 时,
时,  的最大值是
的最大值是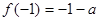
当 时,
时, 的最大值是
的最大值是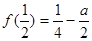 10分
10分
考点:本题主要考查分段函数的奇偶性、单调性和最值问题的综合运用能力,考查数形结合、分类与整合思想。
点评:中档题,分段函数是高考考查的重点函数类型之一,在不同范围内,函数表达式不同,能有效地扩大考查知识的覆盖面。二次函数的图象和性质也是高考考查的重点。更是阶段考试的主要题型。

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
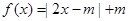 .
. 的解集为
的解集为 ,求实数
,求实数 的值;
的值;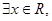 使
使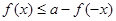 能成立,求实数a的取值范围.
能成立,求实数a的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;
的值; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.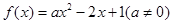 .
.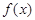 有两个零点,求
有两个零点,求 的取值范围;
的取值范围;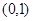 与
与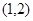 上各有一个零点,求
上各有一个零点,求 (
(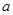 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数 是区间[-1,1]上的减函数
是区间[-1,1]上的减函数 的取值范围;
的取值范围; 在
在 上恒成立,求
上恒成立,求 的取值范围。
的取值范围。 的定义域.
的定义域. 是定义在
是定义在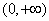 上的单调增函数,满足
上的单调增函数,满足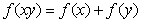 ,
,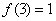 ;
;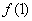 ;
; 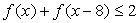 ,求
,求 的取值范围。
的取值范围。