题目内容
下列命题正确的有（ ）①对任意实数a、b，都有|a+b|+|a-b|≥2a
②函数y=x
（0＜x＜1）的最大函数值为
；③对a∈R，不等式|x|＜a的解集可表示为{x|-a＜x＜a}；
④若AB≠0，则lg
≥
．A．①②④
B．③④
C．②③
D．①④
【答案】分析：①根据绝对值不等式来判断．②利用基本不等式或二次函数的性质判断．③利用绝对值不等式的解法判断．④利用基本不等式以及对数函数的单调性判断．
解答：解：①根据绝对值不等式的性质可知对任意实数a、b，都有|a+b|+|a-b|≥|a+b+a-b|=2|a|≥2a，所以①正确．
②因为0＜x＜1，所以y=x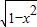
≤
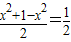，当且仅当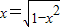
，解得2x2=1，x=
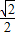时取等号，所以②正确．
③当a≤0时，不等式|x|＜a的解集为空集，所以③错误．
④因为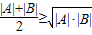
，所以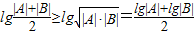
所以④正确．
故正确的是①②④．
故选A．
点评：本题主要考查了命题的真假判断以及不等式的解法和应用．
解答：解：①根据绝对值不等式的性质可知对任意实数a、b，都有|a+b|+|a-b|≥|a+b+a-b|=2|a|≥2a，所以①正确．
②因为0＜x＜1，所以y=x
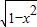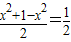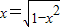≤，当且仅当，解得2x2=1，x=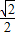时取等号，所以②正确．③当a≤0时，不等式|x|＜a的解集为空集，所以③错误．
④因为
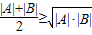，所以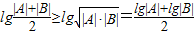所以④正确．故正确的是①②④．
故选A．
点评：本题主要考查了命题的真假判断以及不等式的解法和应用．
练习册系列答案
相关题目