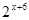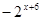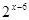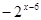题目内容
已知函数f(x)=x2+ax+b,且f(x+2)是偶函数,则f(1),f(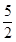 ),f(
),f(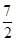 )的大小关系是( )
)的大小关系是( )
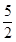 ),f(
),f(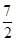 )的大小关系是( )
)的大小关系是( )A.f(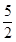 )<f(1)<f( )<f(1)<f(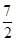 ) ) | B.f(1)<f(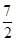 )<f( )<f(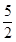 ) ) |
C.f(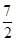 )<f(1)<f( )<f(1)<f(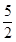 ) ) | D.f(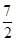 )<f( )<f(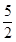 )<f(1) )<f(1) |
A
解:∵f(x+2)是偶函数∴函数f(x)=x2+ax+b关于直线x=2对称,∴f(1)=f(3),又该函数图象开口向上,当x>2时单调递增,则f(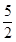 )<f(1)<f(
)<f(1)<f(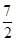 ) ,故选A.
) ,故选A.
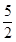 )<f(1)<f(
)<f(1)<f(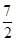 ) ,故选A.
) ,故选A.
练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
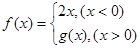 为奇函数,则
为奇函数,则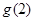 的值为( )
的值为( )



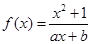 是奇函数,且
是奇函数,且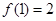 .
. 的表达式;(2) 设
的表达式;(2) 设 ;
; 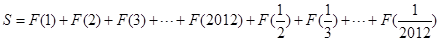 ,求S的值.
,求S的值. 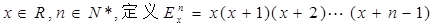 ,例如
,例如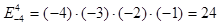 则
则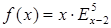 的奇偶性为 ( )
的奇偶性为 ( )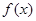 (
(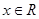 )满足:
)满足: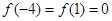 ,且在区间
,且在区间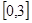 与
与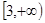 上分别递减和递增,则不等式
上分别递减和递增,则不等式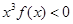 的解集为 ( )
的解集为 ( )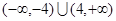
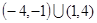
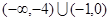
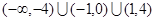
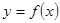 是
是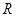 上的奇函数,满足
上的奇函数,满足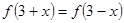 ,当
,当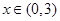 时
时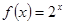
 ,则当
,则当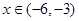 时,
时,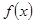 =( )
=( )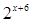
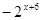
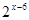
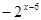
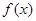 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且 ,则方程
,则方程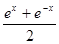
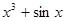
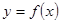 是
是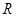 上的奇函数,满足
上的奇函数,满足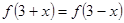 ,当
,当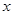 ∈(0,3)时
∈(0,3)时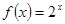
 ,则当
,则当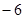 ,
,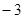 )时,
)时,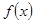 =( )
=( )