题目内容
(本小题满分14分)已知函数 .
.
(Ⅰ)函数 在区间
在区间 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;
(Ⅱ)当 时,
时, 恒成立,求整数
恒成立,求整数 的最大值;
的最大值;
(Ⅲ)试证明: .
.
(1)  在区间
在区间 上是减函数
上是减函数
(2) 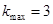
(3)在二问的基础上,进行放缩法来证明不等式。
解析试题分析:解:(Ⅰ)由题 …………2分
…………2分
故 在区间
在区间 上是减函数;…………3分
上是减函数;…………3分
(Ⅱ)当 时,
时, 恒成立,即
恒成立,即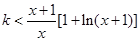 在
在 上恒成立,取
上恒成立,取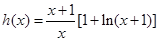 ,则
,则 ,…………………5分
,…………………5分
再取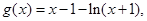 则
则
故 在
在 上单调递增,
上单调递增,
而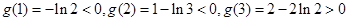 ,…………………7分
,…………………7分
故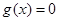 在
在 上存在唯一实数根
上存在唯一实数根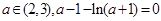 ,
,
故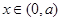 时,
时,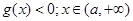 时,
时,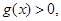
故 故
故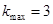 …………………8分
…………………8分
(Ⅲ)由(Ⅱ)知:
令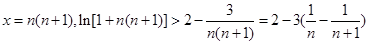 ,………………10分
,………………10分
又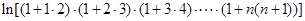
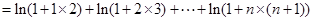
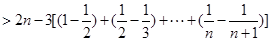 ……………………12分
……………………12分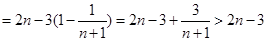
即: ………………14分
………………14分
考点:本试题主要是考查了导数在函数中的应用。
点评:利用导数的正负来判定函数的单调性,并求解函数的最值的应用个。对于含有参数的不等式恒成立问题,一般采用分离变量的思想,借助于函数的最值来得参数的范围。对于函数与不等式的结合问题,一般运用放缩法的思想来求证,属于难度试题。

练习册系列答案
相关题目
 .
. 在点
在点 处的切线方程;
处的切线方程; ,如果过点
,如果过点 可作曲线
可作曲线
 .
. 在点
在点 处的切线方程;
处的切线方程; ,如果过点
,如果过点 可作曲线
可作曲线 .
. 满足0<
满足0< 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; ,
,
 ,
, 是
是 的导函数(
的导函数( 为自然对数的底数)
为自然对数的底数) 的不等式:
的不等式: ;
; ,求实数
,求实数 的取值范围.
的取值范围.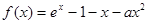
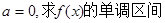 ;
;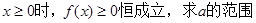
 在
在 处有极值,其图象在
处有极值,其图象在 处的切线与直线
处的切线与直线 平行.
平行. 时,
时, 恒成立,求实数
恒成立,求实数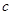 的取值范围。
的取值范围。 为实数,函数
为实数,函数 ,
, .
. 的单调区间与极值;
的单调区间与极值; 且
且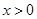 时,
时, .
. (单位:m/s)紧急刹车至停止。求:
(单位:m/s)紧急刹车至停止。求: