题目内容
设max{f(x),g(x)}= ,若函数n(x)=x2+px+q(p,q∈R)的图象经过不同的两点(
,若函数n(x)=x2+px+q(p,q∈R)的图象经过不同的两点( ,0)、(
,0)、( ,0),且存在整数n使得n<
,0),且存在整数n使得n< <
< <n+1成立,则( )
<n+1成立,则( )
| A.max{n(n),n(n+1)}>1 | B.max{n(n),n(n+1)}<1 |
C.max{n(n),n(n+1)}>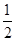 | D.max{n(n),n(n+1)}> 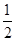 |
B
解析

练习册系列答案
相关题目
若直角坐标平面内的两个不同的点 满足条件:①
满足条件:① 都在函数
都在函数 的图象上;②
的图象上;② 关于原点对称.则称点对
关于原点对称.则称点对 为函数
为函数 的一对“友好点对”.(注:点对
的一对“友好点对”.(注:点对 与
与 为同一“友好点对”).已知函数
为同一“友好点对”).已知函数 ,此函数的友好点对有( )
,此函数的友好点对有( )
| A.0对 | B.1对 | C.2对 | D.3对 |

若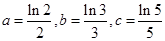 ,则( )
,则( )
A. | B. | C. | D. |
已知 ,
, ,
, 则
则
| A. a>b>c | B.b>a>c | C.a>c>b | D.c>a>b |
若不等式 对任意的
对任意的 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.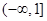 |
若函数y=f(x)图象上的任意一点p的坐标(x,y)满足条件|x|≥|y|,则称函数具有性质S,那么下列函数中具有性质S的是( )
| A.f(x)=tanx | B. -1 -1 |
| C.f(x)=sinx | D.f(x)= ln(x+1) |
设 则
则 的大小关系是( )
的大小关系是( )
A. | B.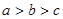 |
C. | D. |
定义max{s1,s2,…,sn}表示实数s1,s2,…,sn中的最大者.设A=(a1,a2,a3),B= ,记A?B=max{a1b1,a2b2,a3b3}.设A=(x-1,x+1,1),B=
,记A?B=max{a1b1,a2b2,a3b3}.设A=(x-1,x+1,1),B= ,若A?B=x-1,则x的取值范围为( )
,若A?B=x-1,则x的取值范围为( )
A.[1- ,1] ,1] |
B.[1,1+ ] ] |
C.[1- ,1] ,1] |
D.[1,1+ ] ] |
设x,y∈R,且4xy+4y2+x+6=0,则x的取值范围是 ( )
| A.-3≤x≤2 | B.-2≤x≤3 |
| C.x≤-2或x≥3 | D.x≤-3或x≥2 |