题目内容
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() .我们将其结论推广:椭圆
.我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用.已知,直线
,在解本题时可以直接应用.已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(1)求![]() 的值
的值
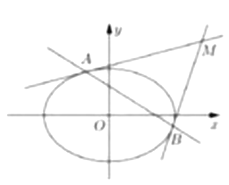
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .当
.当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)联立直线与椭圆方程,根据相切利用判别式即可求解;
(2)求出直线![]() 的方程,求出弦长
的方程,求出弦长![]() 和点
和点![]() 到直线
到直线![]() 的距离,表示出
的距离,表示出![]() 的面积,再求最大值.
的面积,再求最大值.
(1)将直线![]() 代入椭圆方程
代入椭圆方程![]() ,
,
可得:![]() ,
,
由直线和椭圆相切:![]() ,
,![]() ,
,
解得:![]() ;
;
(2)椭圆方程![]() ,
,
设![]() ,
,
则![]() 两点处的切线分别为:
两点处的切线分别为:
![]() ,
,![]() ,两条直线交于点
,两条直线交于点![]() ,
,
则![]() ,
,![]() ,即
,即![]() 两点在直线
两点在直线![]() 上,
上,
所以直线![]() 的方程为
的方程为![]() ,
,
所以![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
由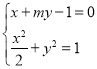 得:
得:![]() ,
,![]() 是方程的两根,
是方程的两根,
![]() ,
,
![]()
![]()
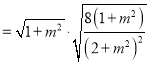
![]() ,
,
所以![]() 的面积:
的面积:
![]()
![]()
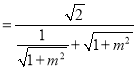 ,
,
根据基本不等式![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
所以![]() 的面积
的面积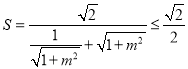 ,
,
当且仅当![]() 时面积取得最大值
时面积取得最大值![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某农户计划种植莴笋和西红柿,种植面积不超过![]() 亩,投入资金不超过
亩,投入资金不超过![]() 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为____万元