题目内容
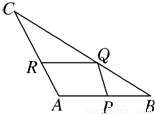
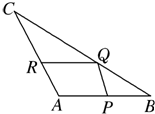如图，△ABC是一块边长AB=3m，AC=5m，BC=7m的剩余角料．现要从中裁剪出一块面积最大的平行四边形用料APQR，要求顶点P，Q，R分别在边AB，BC，CA上．问点Q在BC边上的什么位置时，剪裁符合要求？并求这个最大值．
分析：先利用正弦定理，求出PQ，RQ，再表达出平行四边形的面积，从而求出面积的最大值．
解答：解：设BQ=x，则CQ=7-x，且0＜x＜7．
由余弦定理，得A=120°，cosB=
，cosC=
，
∴sinB=
，sinC=
．
在△PQB中，由正弦定理，得PQ=
．
在△RQC中，由正弦定理，得RQ=
．
∴S?APQR=PQ•RQ•sin120°=
=
x（7-x），当x=
时，取最大值
．
故当Q是BC中点时，平行四边形APQR面积最大，最大面积为
米．
由余弦定理，得A=120°，cosB=
| 11 |
| 14 |
| 13 |
| 14 |
∴sinB=
5
| ||
| 14 |
3
| ||
| 14 |
在△PQB中，由正弦定理，得PQ=
| xsinB |
| sin120° |
在△RQC中，由正弦定理，得RQ=
| (7-x)sinC |
| sin120° |
∴S?APQR=PQ•RQ•sin120°=
| x(7-x)sinBsinC |
| sin120° |
=
15
| ||
| 98 |
| 7 |
| 2 |
15
| ||
| 8 |
故当Q是BC中点时，平行四边形APQR面积最大，最大面积为
15
| ||
| 8 |
点评：本题主要考查正弦定理得运用，及利用二次函数（或基本不等式）求最值，属于中档题．
练习册系列答案
相关题目
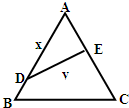如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．