题目内容
如图,△ABC是形状为正三角形的一块地,为了绿化需要现在线段AB上取一点P,在AC上取一点Q,用直线段或折线段或曲线段连接PQ,将△ABC分为面积相等的两块地,分别种上两种花草.
(1)如果用直线段连接PQ,那么当P、Q处于什么位置时,线段PQ的长度最小?
(2)请你设计连接PQ的一种方式,使得连接PQ的长度比(1)中计算的长度更小.
(1)如果用直线段连接PQ,那么当P、Q处于什么位置时,线段PQ的长度最小?
(2)请你设计连接PQ的一种方式,使得连接PQ的长度比(1)中计算的长度更小.
分析:(1)设AP=a,AQ=b,正三角形的边长为c,根据PQ将△ABC分为面积相等的两块地,可得ab=
c2,利用基本不等式可求PQ的最小值;
(2)若AP为圆弧,则设AP=a,PQ=
a,根据PQ将△ABC分为面积相等的两块地,可求弧PQ的长度,比较可得答案.
| 1 |
| 2 |
(2)若AP为圆弧,则设AP=a,PQ=
| π |
| 3 |
解答:解:(1)设AP=a,AQ=b,正三角形的边长为c,则
∵PQ将△ABC分为面积相等的两块地
∴ab=
c2
∴PQ2=a2+b2-ab≥ab=
c2
当且仅当a=b=
c时,PQ取得最小为
c,此时AP=AQ=
AB
(2)若AP为圆弧,则设AP=a,PQ=
a,
∵PQ将△ABC分为面积相等的两块地
∴
πa2=
c2
∴a2=
c2
∴PQ2=
c2<
c2
故满足题意.
∵PQ将△ABC分为面积相等的两块地
∴ab=
| 1 |
| 2 |
∴PQ2=a2+b2-ab≥ab=
| 1 |
| 2 |
当且仅当a=b=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)若AP为圆弧,则设AP=a,PQ=
| π |
| 3 |
∵PQ将△ABC分为面积相等的两块地
∴
| 1 |
| 6 |
| ||
| 8 |
∴a2=
3
| ||
| 4π |
∴PQ2=
| ||
| 12 |
| 1 |
| 2 |
故满足题意.
点评:本题以实际问题为载体,考查优化设计,考查了基本不等式的运用,考查扇形的弧长及面积公式.

练习册系列答案
相关题目
 (2013•湛江二模)如图,已知平面上直线l1∥l2,A、B分别是l1、l2上的动点,C是l1,l2之间一定点,C到l1的距离CM=1,C到l2的距离CN=
(2013•湛江二模)如图,已知平面上直线l1∥l2,A、B分别是l1、l2上的动点,C是l1,l2之间一定点,C到l1的距离CM=1,C到l2的距离CN= (2003•东城区二模)将三棱锥P-ABC(如图甲)沿三条侧棱剪开后,展开成如图乙的形状,其中P1,B,P2共线,P2,C,P3共线,且P1P2=P2P3,则在三棱锥P-ABC中,PA与BC所成的角的大小是
(2003•东城区二模)将三棱锥P-ABC(如图甲)沿三条侧棱剪开后,展开成如图乙的形状,其中P1,B,P2共线,P2,C,P3共线,且P1P2=P2P3,则在三棱锥P-ABC中,PA与BC所成的角的大小是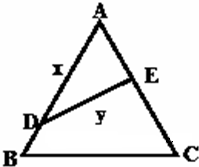 有一展馆形状是边长为2的等边三角形ABC,DE把展馆分成上下两部分面积比为1:2(如图所示),其中D在AB上,E在AC上.
有一展馆形状是边长为2的等边三角形ABC,DE把展馆分成上下两部分面积比为1:2(如图所示),其中D在AB上,E在AC上.