题目内容
已知P、A、B、C是平面内四个不同的点，且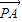
+
+
=
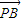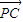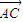，则（ ）A．C三点共线
B．P三点共线
C．P三点共线
D．P三点共线
【答案】分析：根据已知式子和选项的特点，把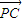 
移到另一边，再由相反向量知 
=-
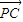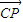，利用向量加法的首尾相连进行化简，再用同样的方法化简得到
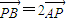，最后即可解决问题．
解答：解：∵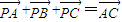
，
∴
+
=
-
=
+
=
，
∴
=
-
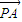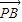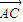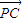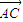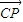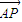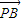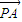=2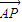 
．
故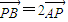
，从而三点P，B，A共线
故选B．
点评：本题考查向量加法的首尾相连法则和相反向量的定义，是基础题．
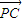移到另一边，再由相反向量知 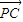=-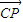，利用向量加法的首尾相连进行化简，再用同样的方法化简得到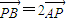，最后即可解决问题．解答：解：∵
，∴
+=-=+=，∴
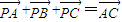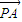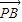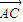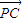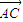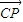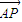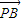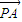=-=2 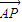．故
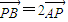，从而三点P，B，A共线故选B．
点评：本题考查向量加法的首尾相连法则和相反向量的定义，是基础题．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
已知P，A，B，C是平面内四点，且
+
+
=
，那么一定有（ ）
| PA |
| PB |
| PC |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知P、A、B、C是平面内四个不同的点，且
+
+
=
，则（ ）
| PA |
| PB |
| PC |
| AC |
| A、C三点共线 |
| B、P三点共线 |
| C、P三点共线 |
| D、P三点共线 |