题目内容
设函数f(x)=lnx-ax+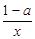 -1.
-1.
(1) 当a=1时, 过原点的直线与函数f(x)的图象相切于点P, 求点P的坐标;
(2) 当0<a<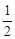 时, 求函数f(x)的单调区间;
时, 求函数f(x)的单调区间;
(3) 当a=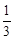 时, 设函数g(x)=x2-2bx-
时, 设函数g(x)=x2-2bx-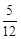 , 若对于
, 若对于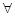 x1∈
x1∈ ,
, 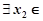 [0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<
[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<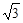 +1).
+1).
【答案】
(1)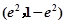 (2) 增区间为
(2) 增区间为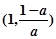 减区间为
减区间为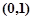 ,
,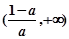 (3)
(3)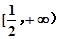
【解析】
试题分析:函数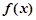 的定义域为
的定义域为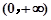 ,
,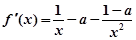 (2分)
(2分)
(1)设点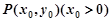 ,当
,当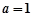 时,
时,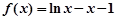 ,则
,则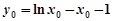 ,
,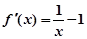 ,∴
,∴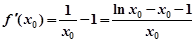 (3分)
(3分)
解得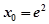 ,故点P 的坐标为
,故点P 的坐标为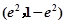 (4分)
(4分)
(2)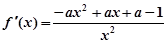
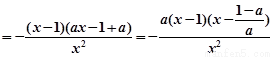
∵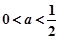 ∴
∴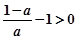 (6分)
(6分)
∴当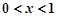 ,或
,或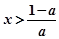 时
时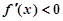 ,当
,当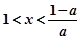 时,
时,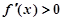
故当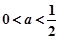 时,函数
时,函数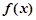 的单调递增区间为
的单调递增区间为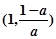 ;
;
单调递减区间为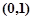 ,
,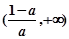 (8分)
(8分)
(3)当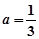 时,
时, 由(Ⅱ)可知函数
由(Ⅱ)可知函数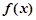 在
在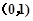 上是减函数,在
上是减函数,在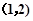 上为增函数,在
上为增函数,在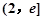 上为减函数,且
上为减函数,且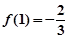 ,
,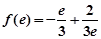
∵ ,又
,又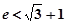 ,∴
,∴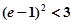 ,
,
∴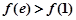 ,故函数
,故函数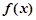 在
在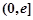 上的最小值为
上的最小值为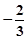 (10分)
(10分)
若对于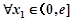 ,
,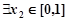 使
使 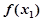 ≥
≥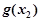 成立
成立
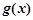 在
在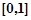 上的最小值不大于
上的最小值不大于
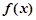 在
在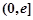 上的最小值
上的最小值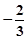 (*) (11分)
(*) (11分)
又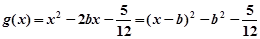 ,
,
①当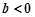 时,
时,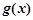 在
在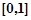 上为增函数,
上为增函数, 与(*)矛盾
与(*)矛盾
②当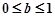 时,
时,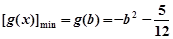 ,由
,由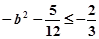 及
及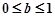 得,
得,
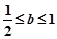
③当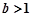 时,
时,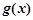 在
在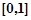 上为减函数,
上为减函数,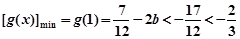 ,
,
此时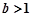
综上,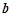 的取值范围是
的取值范围是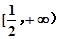 (14分)
(14分)
考点:曲线的切线,函数单调性最值
点评:第一问函数曲线与某直线相切时,充分利用切点坐标与直线曲线的联系寻求关系式,第二问求单调区间主要通过导数的正负分别求得单调增减区间,第三问首先将不等式问题转化为函数最值问题,须认真分析清楚需要比较的是最大值还是最小值,这一点是容易出错的地方

练习册系列答案
相关题目