题目内容
设函数f(x)=ln(x+1)-
的零点为x0,若x0∈(k,k+1),k为整数,则k的值等于
| 2 | x |
-1或1
-1或1
.分析:方程f(x)=ln(x+1)-
=0的解个数,可看成y=ln(x+1)与y=
的交点个数,在同一坐标系下作出函数y=ln(x+1)与y=
的图象,结合函数零点的判定定理可得结论.
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
解答:解:方程f(x)=ln(x+1)-
=0的解个数,可看成y=ln(x+1)与y=
的交点个数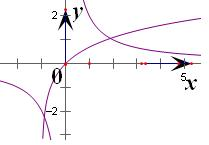
在同一坐标系下作出函数y=ln(x+1)与y=
的图象
根据图象可知其中一个交点横坐标在区间(-1,0)
而f(1)=ln2-2<0,f(2)=ln3-1>0
则f(1)f(2)<0
∴f(x)=ln(x+1)-
的零点为x0∈(1,2),
故答案为:-1或1
| 2 |
| x |
| 2 |
| x |

在同一坐标系下作出函数y=ln(x+1)与y=
| 2 |
| x |
根据图象可知其中一个交点横坐标在区间(-1,0)
而f(1)=ln2-2<0,f(2)=ln3-1>0
则f(1)f(2)<0
∴f(x)=ln(x+1)-
| 2 |
| x |
故答案为:-1或1
点评:本题考查函数的零点的判定定理,以及数形结合法的应用和转化的思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目