题目内容
已知点P(4, 4),圆C: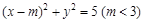 与椭圆E:
与椭圆E: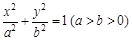 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.

(Ⅰ)求m的值与椭圆E的方程;(Ⅱ)设Q为椭圆E上的一个动点,求 的取值范围.
的取值范围.
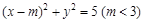 与椭圆E:
与椭圆E: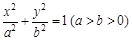 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
(Ⅰ)求m的值与椭圆E的方程;(Ⅱ)设Q为椭圆E上的一个动点,求
 的取值范围.
的取值范围.(1)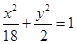 。
。
(2)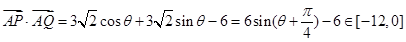 。
。
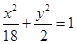 。
。(2)
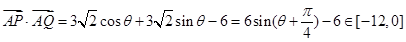 。
。试题分析:(1)代入点A(3,1)得m=1或5,得m=1 2分
设PF
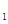 斜率为k,
斜率为k,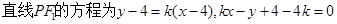
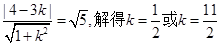 5分
5分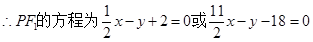
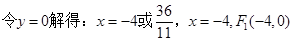 7分
7分列方程组得:
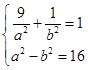 解得:
解得: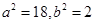
所求椭圆方程为
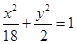 10分
10分(2)设点Q
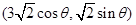 12分
12分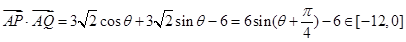 16分
16分点评:中档题,求椭圆的标准方程,主要运用了椭圆的几何性质,a,b,c,e的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理,简化解题过程。通过向量的坐标运算,得到三角函数式,应用辅助角公式“化一”后,确定数量积的范围。

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 分别是椭圆
分别是椭圆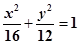 的左、右焦点,点P在椭圆上,若△
的左、右焦点,点P在椭圆上,若△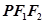 为直角三角形,则△
为直角三角形,则△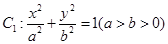 与直线
与直线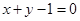 相交于
相交于 两点.
两点.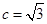 ,直线
,直线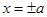 与
与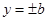 围成的矩形
围成的矩形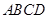 的面积为8,
的面积为8,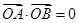 (
(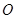 为坐标原点),求证:
为坐标原点),求证: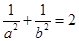 ;
;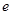 满足
满足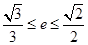 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围. 中,
中,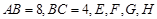 分别为四边的中点,且都在坐标轴上,设
分别为四边的中点,且都在坐标轴上,设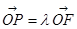 ,
,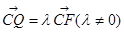 .
.
 与
与 的交点
的交点 的轨迹
的轨迹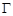 的方程;
的方程;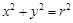
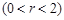 上一点
上一点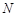 作圆的切线与轨迹
作圆的切线与轨迹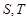 两点,若
两点,若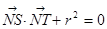 ,试求出
,试求出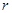 的值.
的值.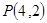 是直线
是直线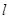 被椭圆
被椭圆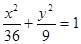 所截得的线段中点,求直线
所截得的线段中点,求直线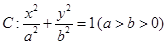 .
.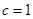 ,且
,且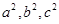 成等差数列,求椭圆
成等差数列,求椭圆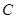 的方程;
的方程;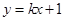 相交于
相交于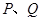 两点,求
两点,求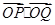 的取值范围.
的取值范围.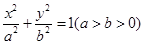 的四个顶点A、B、C、D, 若菱形ABCD的内切圆恰好经过椭圆的焦点, 则椭圆的离心率为 __ .
的四个顶点A、B、C、D, 若菱形ABCD的内切圆恰好经过椭圆的焦点, 则椭圆的离心率为 __ .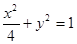 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.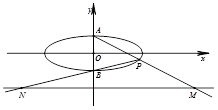
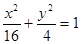 上有两点P、Q ,O为原点,若OP、OQ斜率之积为
上有两点P、Q ,O为原点,若OP、OQ斜率之积为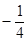 ,
,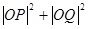 等于( )
等于( )