题目内容
(重点班)我们知道对数函数 ,对任意
,对任意 ,都有
,都有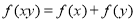 成立,若
成立,若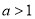 ,则当
,则当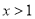 时,
时, .参照对数函数的性质,研究下题:定义在
.参照对数函数的性质,研究下题:定义在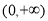 上的函数
上的函数 对任意
对任意 ,都有
,都有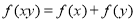 ,并且当且仅当
,并且当且仅当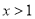 时,
时, 成立.
成立.
(1)设 ,求证:
,求证: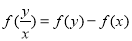 ;
;
(2)设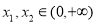 ,若
,若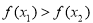 ,比较
,比较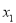 与
与 的大小.
的大小.
练习册系列答案
相关题目
题目内容
(重点班)我们知道对数函数 ,对任意
,对任意 ,都有
,都有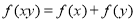 成立,若
成立,若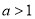 ,则当
,则当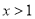 时,
时, .参照对数函数的性质,研究下题:定义在
.参照对数函数的性质,研究下题:定义在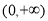 上的函数
上的函数 对任意
对任意 ,都有
,都有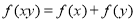 ,并且当且仅当
,并且当且仅当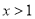 时,
时, 成立.
成立.
(1)设 ,求证:
,求证: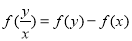 ;
;
(2)设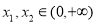 ,若
,若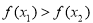 ,比较
,比较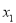 与
与 的大小.
的大小.