题目内容
(本题满分13分)
已知函数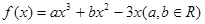 ,在点
,在点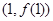 处的切线方程为
处的切线方程为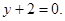
(1)求函数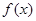 的解析式;
的解析式;
(2)若对于区间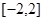 上任意两个自变量的值
上任意两个自变量的值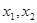 ,都有
,都有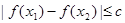 ,求实数
,求实数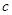 的最小值。
的最小值。
(3)若过点 ,可作曲线
,可作曲线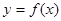 的三条切线,求实数
的三条切线,求实数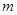 的取值范围。
的取值范围。
【答案】
(1) 1分
1分
根据题意,得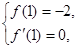
即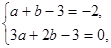
解得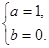 2分
2分
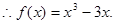 3分
3分
(2)令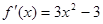
即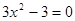 ,解得
,解得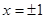
|
|
-2 |
|
-1 |
(-1,1) |
1 |
(1,2) |
2 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
-2 |
|
极大值 |
|
极小值 |
|
2 |

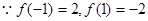
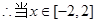 时,
时,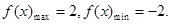
则对于区间[-2,2]上任意两个自变量的值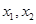 ,都有
,都有
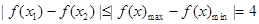
所以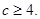
所以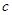 的最小值为4。
7分
的最小值为4。
7分
(Ⅲ)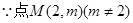 不在曲线
不在曲线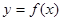 上。
上。
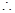 设切点为
设切点为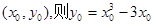
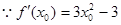 ,
,
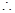 切线的斜率为
切线的斜率为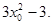 8分
8分
则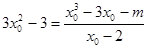 9分
9分
即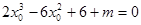 ,
,
因为过点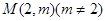 ,可作曲线
,可作曲线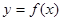 的三条切线
的三条切线
所以方程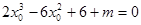 有三个不同的实数解 10分
有三个不同的实数解 10分
即函数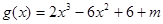 有三个不同的零点,
有三个不同的零点,
则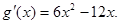
令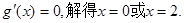
|
|
|
0 |
(0,2) |
2 |
(2,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
注:若有其它解未能,请酌情给分。
【解析】略

练习册系列答案
相关题目
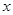
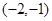
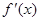
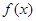


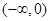
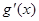
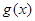



 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.