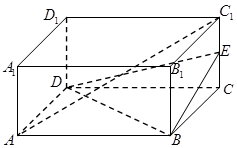题目内容
在三棱锥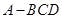 中,侧棱
中,侧棱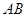 、
、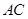 、
、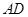 两两垂直,
两两垂直,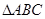 、
、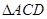 、
、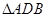 的面积分别为
的面积分别为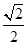 、
、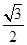 、
、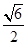 ,则该三棱锥外接球的表面积为
,则该三棱锥外接球的表面积为
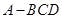 中,侧棱
中,侧棱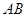 、
、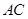 、
、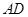 两两垂直,
两两垂直,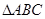 、
、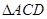 、
、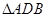 的面积分别为
的面积分别为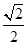 、
、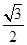 、
、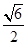 ,则该三棱锥外接球的表面积为
,则该三棱锥外接球的表面积为A.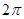 | B.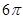 | C.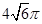 | D.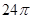 |
B
因为侧棱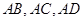 两两垂直,所以三棱锥
两两垂直,所以三棱锥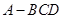 可以视作长方体的一角。因为
可以视作长方体的一角。因为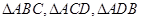 的面积分别为
的面积分别为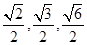 ,所以可得长方体的长,宽和高分别为
,所以可得长方体的长,宽和高分别为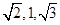 。则该三棱锥的外接球即长方体的外接球的直径等于长方体的体对角线长,即
。则该三棱锥的外接球即长方体的外接球的直径等于长方体的体对角线长,即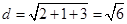 ,所以表面积
,所以表面积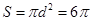 ,故选B
,故选B
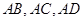 两两垂直,所以三棱锥
两两垂直,所以三棱锥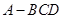 可以视作长方体的一角。因为
可以视作长方体的一角。因为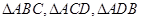 的面积分别为
的面积分别为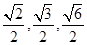 ,所以可得长方体的长,宽和高分别为
,所以可得长方体的长,宽和高分别为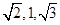 。则该三棱锥的外接球即长方体的外接球的直径等于长方体的体对角线长,即
。则该三棱锥的外接球即长方体的外接球的直径等于长方体的体对角线长,即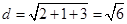 ,所以表面积
,所以表面积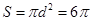 ,故选B
,故选B
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
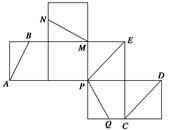
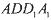 中,点B、C在线段AD上,且AB = 3,BC = 4,作
中,点B、C在线段AD上,且AB = 3,BC = 4,作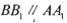 分别交
分别交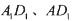 于点B,P,作
于点B,P,作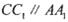 分别交
分别交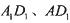 于点
于点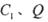 ,将该正方形沿
,将该正方形沿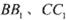 折叠,使得
折叠,使得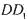 与
与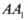 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱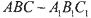
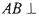 平面
平面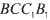 ;
;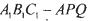 的体积.
的体积.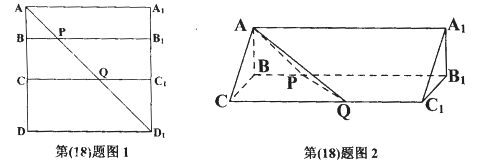
 与平面
与平面 ,有以下四个命题:①若
,有以下四个命题:①若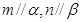 且
且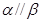 ,则
,则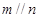 ;
;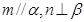 且
且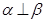 ,则
,则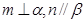 且
且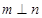 ;
;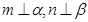 且
且 的长方体被截面
的长方体被截面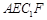 所截
所截 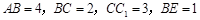 .
. ;
;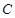 到平面
到平面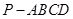 中,底面
中,底面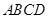 是平行四边形,
是平行四边形,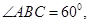
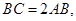
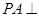 底面
底面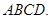
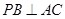 ;(Ⅱ)若
;(Ⅱ)若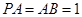 ,求二面角
,求二面角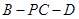 的余弦值;
的余弦值;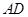 上是否存在一点
上是否存在一点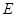 使二面角
使二面角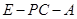 为
为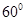 ,若存在,试确定点
,若存在,试确定点
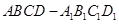 中,
中, 为
为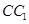 的中点.
的中点.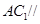 平面
平面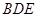 ;
;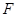 在棱
在棱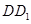 上什么位置时,平面
上什么位置时,平面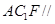 平面
平面