题目内容
(本小题共12分)
在如图的多面体中,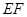 ⊥平面
⊥平面 ,
, ,
,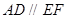 ,
,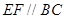 ,
,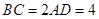 ,
,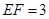 ,
,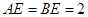 ,
, 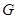 是
是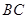 的中点.
的中点.
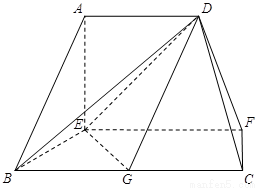
(Ⅰ)求证: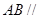 平面
平面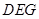 ;
;
(Ⅱ)求证: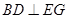 ;
;
【答案】
(Ⅰ)∵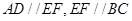 , ∴
, ∴ . 又∵
. 又∵ ,
,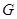 是
是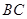 的中点, ∴
的中点, ∴ ,∴四边形
,∴四边形 是平行四边形,∴
是平行四边形,∴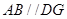 . ∵
. ∵ 平面
平面 ,
,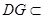 平面
平面 ,∴
,∴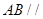 平面
平面 .
.
(Ⅱ)∵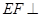 平面
平面 ,
,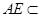 平面
平面 ,∴
,∴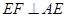 ,又
,又 ,
,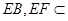 平面
平面 ,∴
,∴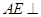 平面
平面 .过
.过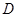 作
作 交
交 于
于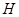 ,则
,则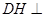 平面
平面 .∵
.∵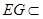 平面
平面 , ∴
, ∴ .∵
.∵ ,∴四边形
,∴四边形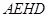 平行四边形,∴
平行四边形,∴ ,∴
,∴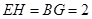 ,又
,又 ,
,
∴四边形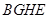 为正方形,∴
为正方形,∴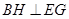 ,又
,又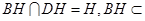 平面
平面 ,
,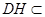 平面
平面 ,∴
,∴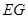 ⊥平面
⊥平面 .∵
.∵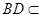 平面
平面 ,∴
,∴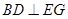 .
.
【解析】
试题分析:(Ⅰ)证明:∵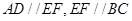 ,
,
∴ .
.

又∵ ,
,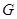 是
是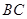 的中点,∴
的中点,∴ ,
,
∴四边形 是平行四边形,∴
是平行四边形,∴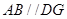 .
.
∵ 平面
平面 ,
,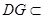 平面
平面 ,∴
,∴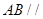 平面
平面 .……………5分
.……………5分
(Ⅱ)∵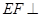 平面
平面 ,
,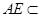 平面
平面 ,∴
,∴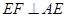 ,
,
又 ,
,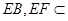 平面
平面 ,
,
∴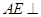 平面
平面 .
.
过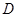 作
作 交
交 于
于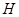 ,则
,则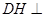 平面
平面 .
.
∵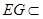 平面
平面 , ∴
, ∴ .
.
∵ ,∴四边形
,∴四边形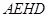 平行四边形,
平行四边形,
∴ ,
,
∴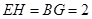 ,又
,又 ,
,
∴四边形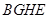 为正方形,∴
为正方形,∴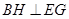 ,
,
又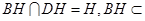 平面
平面 ,
,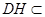 平面
平面 ,
,
∴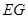 ⊥平面
⊥平面 . ∵
. ∵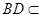 平面
平面 ,∴
,∴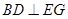 .
………12分
.
………12分
考点:本题考查了空间中的线面关系
点评:高考中常考查空间中平行关系与垂直关系的证明以及几何体体积的计算,这是高考的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理.

练习册系列答案
相关题目
 ⊥平面
⊥平面 ,
, ∥
∥ 是正三角形,
是正三角形, ,且
,且 是
是 的中点
的中点
 ∥平面
∥平面 ;
; .
. 名,女同学有
名,女同学有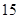 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个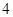 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;


 ,
, ,求证:
,求证: .
. 的值.
的值.