题目内容
定义在(0,+∞)上的函数f(x)满足:①当x∈[1,3)时,f(x)=
;②f(3x)=3f(x).
(i)f(6)=
(ii)若函数F(x)=f(x)-a的零点从小到大依次记为x1,x2,…,xn,…,则当a∈(1,3)时,x1+x2+…+x2n-1+x2n=
|
(i)f(6)=
3
3
;(ii)若函数F(x)=f(x)-a的零点从小到大依次记为x1,x2,…,xn,…,则当a∈(1,3)时,x1+x2+…+x2n-1+x2n=
6(3n-1)
6(3n-1)
.分析:(i)由于f(3x)=3f(x),可得f(6)=3f(2),又当x=2时,f(2)=2-1=1,即可得到f(6).
(ii)如图所示,由题意当x∈[0,1)时,不必考虑.利用已知可得:当x∈[3,6]时,由
∈[1,2],可得f(x)=3f(
),f(x)∈[0,3];同理,当x∈(6,9)时,f(x)∈[0,3];此时f(x)∈[0,3].分别作出y=f(x),y=a,则F(x)=f(x)-a在区间(3,6)和(6,9)上各有一个零点,分别为x1,x2,且满足x1+x2=2×6,依此类推:x3+x4=2×18,…,x2n-1+x2n=2×2×3n.利用等比数列的前n项和公式即可得出.
(ii)如图所示,由题意当x∈[0,1)时,不必考虑.利用已知可得:当x∈[3,6]时,由
| x |
| 3 |
| x |
| 3 |
解答:解:当1≤x≤2时,0≤f(x)≤1;当2<x<3时,0<f(x)<1,可得当x∈[1,3)时,f(x)∈[0,1].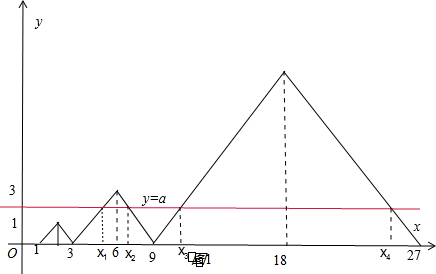
(i)∵f(3x)=3f(x),∴f(6)=3f(2),又当x=2时,f(2)=2-1=1,
∴f(6)=3×1=3.
(ii)当
≤x<1时,则1≤3x<3,由f(x)=
f(3x)可知:f(x)∈[0,
].
同理,当x∈[0,
)时,0≤f(x)<1,因此不必要考虑.
当x∈[3,6]时,由
∈[1,2],可得f(x)=3f(
),f(x)∈[0,3];
同理,当x∈(6,9)时,由
∈(2,3),可得f(x)=3f(
),f(x)∈[0,3];
此时f(x)∈[0,3].作出直线y=a,a∈(1,3).
则F(x)=f(x)-a在区间(3,6)和(6,9)上各有一个零点,分别为x1,x2,且满足x1+x2=2×6,
依此类推:x3+x4=2×18,…,x2n-1+x2n=2×2×3n.
∴当a∈(1,3)时,x1+x2+…+x2n-1+x2n=4×(3+32+…+3n)=4×
=6×(3n-1).

(i)∵f(3x)=3f(x),∴f(6)=3f(2),又当x=2时,f(2)=2-1=1,
∴f(6)=3×1=3.
(ii)当
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
同理,当x∈[0,
| 1 |
| 3 |
当x∈[3,6]时,由
| x |
| 3 |
| x |
| 3 |
同理,当x∈(6,9)时,由
| x |
| 3 |
| x |
| 3 |
此时f(x)∈[0,3].作出直线y=a,a∈(1,3).
则F(x)=f(x)-a在区间(3,6)和(6,9)上各有一个零点,分别为x1,x2,且满足x1+x2=2×6,
依此类推:x3+x4=2×18,…,x2n-1+x2n=2×2×3n.
∴当a∈(1,3)时,x1+x2+…+x2n-1+x2n=4×(3+32+…+3n)=4×
| 3(3n-1) |
| 3-1 |
点评:本题考查了函数的图象与性质、区间转换、对称性、等比数列的前n项和公式等基础知识与基本技能,属于难题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知定义在(0,1)上的函数f(x),对任意的m,n∈(1,+∞)且m<n时,都有f(
)-f(
)=f(
)记an=f(
),n∈N*,则在数列{an}中,a1+a2+…a8=( )
| 1 |
| n |
| 1 |
| m |
| m-n |
| 1-mn |
| 1 |
| n2+5n+5 |
A、f(
| ||
B、f(
| ||
C、f(
| ||
D、f(
|