题目内容
【题目】已知关于x的方程x2-2mx+4m2-6=0的两不等根为α,β,试求(α-1)2+(β-1)2的最值.
【答案】最大值为15,无最小值.
【解析】试题分析:根据一元二次方程写出韦达定理,将原式化简为两根和与乘积的形式代入,化简为关于m的二次函数,由Δ>0求出m的取值范围,即函数的定义域,根据二次函数的图象和性质求出最值.
试题解析:
由题可知α+β=2m,αβ=4m2-6,
∴(α-1)2+(β-1)2=α2+β2-2(α+β)+2=(α+β)2-2αβ-2(α+β)+2
=4m2-2(4m2-6)-2·2m+2=-4m2-4m+14=-4(m+![]() )2+15.
)2+15.
∵Δ=(-2m)2-4(4m2-6)=-12m2+24>0,∴当m=-![]() 时满足Δ>0.∴原式的最大值为15,无最小值.
时满足Δ>0.∴原式的最大值为15,无最小值.
点睛:本题考查一元二次方程根与系数的关系.设一元二次方程![]() 的两根为
的两根为![]() ,
, ![]() ,当
,当![]() 时,方程有两个等根,当
时,方程有两个等根,当![]() 时,方程无根, 当
时,方程无根, 当![]() 时,方程有两个不相等的实数根,且根据韦达定理有
时,方程有两个不相等的实数根,且根据韦达定理有![]() ,或者根据求根公式可得
,或者根据求根公式可得![]() .
.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
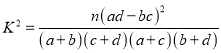
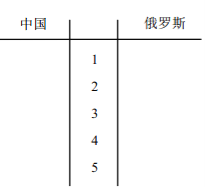
【题目】第![]() 届夏季奥林匹克运动会将于 2016 年 8 月 5 日—21 日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据( 单位: 枚).
届夏季奥林匹克运动会将于 2016 年 8 月 5 日—21 日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据( 单位: 枚).
第 | 第 | 第 | 第 | 第 | |
中国 |
|
|
|
|
|
俄罗斯 |
|
|
|
|
|
(1)根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图, 并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度( 不要求计算出具体数值, 给出结论即可);
(2)甲、 乙、 丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多( 假设两国代表团获得的金牌数不会相等) , 规定甲、 乙、 丙必须在两个代表团中选一个, 已知甲、 乙猜中国代表团的概率都为![]() , 丙猜中国代表团的概率为
, 丙猜中国代表团的概率为![]() , 三人各自猜哪个代表团的结果互不影响.现让甲、 乙、 丙各猜一次, 设三人中猜中国代表团的人数为
, 三人各自猜哪个代表团的结果互不影响.现让甲、 乙、 丙各猜一次, 设三人中猜中国代表团的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
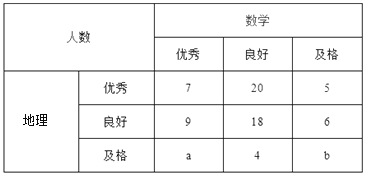
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过![]() 的有20人,不超过
的有20人,不超过![]() 的有10人.在20名女性驾驶员中,平均车速超过
的有10人.在20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过![]() 的人与性别有关;
的人与性别有关;
平均车速超过
| 平均车速不超过
| 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
(Ⅱ )以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为女性且车速不超过![]() 的车辆数为
的车辆数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: ![]() ,其中
,其中![]() .
.
参考数据:
| 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |