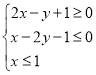题目内容
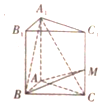
【题目】已知:![]() 中,顶点
中,顶点![]() ,边AB上的中线CD所在直线的方程是
,边AB上的中线CD所在直线的方程是![]() ,边AC上的高BE所在直线的方程是
,边AC上的高BE所在直线的方程是![]() .
.
![]() 求点B、C的坐标;
求点B、C的坐标;
![]() 求
求![]() 的外接圆的方程.
的外接圆的方程.
【答案】(1)![]()
![]() (2)
(2)![]() 或
或![]()
【解析】
试题(1)求![]() ,
,![]() 点就设
点就设![]() ,
,![]() 点的坐标,同时可以表示出
点的坐标,同时可以表示出![]() 的坐标,根据
的坐标,根据![]() 在
在![]() 上,且
上,且![]() 中点
中点![]() 在
在![]() 上.两式联立可求出
上.两式联立可求出![]() ;根据
;根据![]() 在
在![]() 上,且
上,且![]() 得到
得到![]() ,两式联立可求出
,两式联立可求出![]() .
.
(2)所求的圆经过三角形的三个顶点,所以设出圆的一般方程,将![]() ,
,![]() ,
,![]() 代入解方程组即可得到所求圆的方程.或者根据三角形的外接圆的圆心是各边垂直平分线的交点,所以可以根据(1)中的
代入解方程组即可得到所求圆的方程.或者根据三角形的外接圆的圆心是各边垂直平分线的交点,所以可以根据(1)中的![]() ,
,![]() 和已知的
和已知的![]() 求两个边的垂直平分线,取其交点做圆心,该点到各个顶点的距离为半径,求出圆的方程.
求两个边的垂直平分线,取其交点做圆心,该点到各个顶点的距离为半径,求出圆的方程.
试题解析:(1)由题意可设![]() ,则
,则![]() 的中点
的中点![]() .
.
因为![]() 的中点
的中点![]() 必在直线
必在直线![]() 上,代入有
上,代入有![]() ①
①
又因为![]() 在直线
在直线![]() 上,所以代入有
上,所以代入有![]() ②
②
由①②联立解得![]() .则
.则![]() ,
,
因为![]() 在直线
在直线![]() 上,代入有
上,代入有![]() ③
③
又因为直线![]() ,所以有
,所以有![]() ,则有
,则有![]() ④
④
根据③④有![]() .
.
(2)因为三角形外接圆的圆心是各边垂直平分线的交点,
所以找到三角形两边的垂直平分线求得的交点就是外接圆的圆心,该点到各顶点的距离就是半径.
根据![]() 两点,可得斜率为
两点,可得斜率为![]() ,所以中垂线斜率为
,所以中垂线斜率为![]() ,
,![]() 中点为
中点为![]() ,则中垂线为
,则中垂线为![]() ⑤
⑤
同理可得直线![]() 的中垂线为
的中垂线为![]() ⑥,
⑥,
由⑤⑥可得圆心![]() ,半径为
,半径为![]() ,所以外接圆为
,所以外接圆为![]()
法二:(2)设![]() 外接圆的方程为
外接圆的方程为![]() ,其中
,其中![]() 。
。
因为三角形的个顶点都在圆上,所以根据(1),将三点坐标代入有:
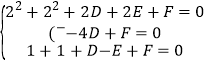 解得
解得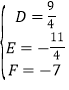
∴![]() 外接圆的方程为
外接圆的方程为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】下表是一个容量为20的样本数据分组后的频率分布表:
分组 | [8.5,11.5] | [11.5,14.5] | [14.5,17.5] | [17.5,20.5] |
频数 | 4 | 2 | 6 | 8 |
(I)若用组中值代替本组数据的平均数,请计算样本的平均数![]() ;
;
(II)以频率估计概率,若样本的容量为2000,求在分组[14.5,17.5)中的频数;
(Ⅲ)若从数据在分组[8.5,11.5)与分组[11.5,14.5)的样本中随机抽取2个,求恰有1个样本落在分组[11.5,14.5)的概率。