题目内容
设z1=m+(2-m2)i, z2=cosθ+(λ+sinθ)i, 其中m,λ,θ∈R,已知z1=2z2,求λ的取值范围.
λ的取值范围是[-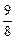 ,2]
,2]
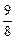 ,2]
,2]解法一:∵z1=2z2,
∴m+(2-m2)i=2cosθ+(2λ+2sinθ)i,∴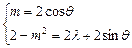
∴λ=1-2cos2θ-sinθ=2sin2θ-sinθ-1=2(sinθ-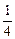 )2-
)2-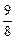 .
.
当sinθ=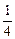 时λ取最小值-
时λ取最小值-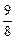 ,当sinθ=-1时,λ取最大值2.
,当sinθ=-1时,λ取最大值2.
解法二:∵z1=2z2 ∴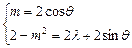
∴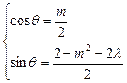 ,
,
∴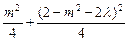 =1.
=1.
∴m4-(3-4λ)m2+4λ2-8λ="0," 设t=m2,则0≤t≤4,
令f(t)=t2-(3-4λ)t+4λ2-8λ,
则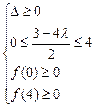 或f(0)·f(4)≤0 ∴
或f(0)·f(4)≤0 ∴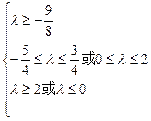
∴-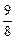 ≤λ≤0或0≤λ≤2.
≤λ≤0或0≤λ≤2.
∴λ的取值范围是[-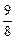 ,2].
,2].
∴m+(2-m2)i=2cosθ+(2λ+2sinθ)i,∴
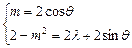
∴λ=1-2cos2θ-sinθ=2sin2θ-sinθ-1=2(sinθ-
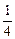 )2-
)2-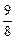 .
.当sinθ=
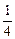 时λ取最小值-
时λ取最小值-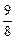 ,当sinθ=-1时,λ取最大值2.
,当sinθ=-1时,λ取最大值2. 解法二:∵z1=2z2 ∴
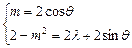
∴
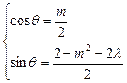 ,
,∴
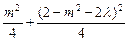 =1.
=1.∴m4-(3-4λ)m2+4λ2-8λ="0," 设t=m2,则0≤t≤4,
令f(t)=t2-(3-4λ)t+4λ2-8λ,
则
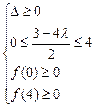 或f(0)·f(4)≤0 ∴
或f(0)·f(4)≤0 ∴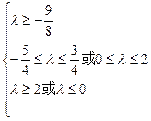
∴-
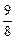 ≤λ≤0或0≤λ≤2.
≤λ≤0或0≤λ≤2.∴λ的取值范围是[-
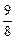 ,2].
,2]. 
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
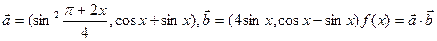
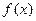 的解析式
的解析式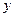 轴的正半轴及
轴的正半轴及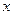 轴的正半轴三者围成图形的面积
轴的正半轴三者围成图形的面积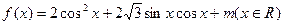
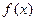 的最小正周期及函数的单调递增区间; (II)若
的最小正周期及函数的单调递增区间; (II)若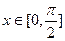 ,是否存在实数m,使函数
,是否存在实数m,使函数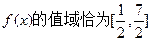 ?若存在,请求出m的取值;若不存在,请说明理由。
?若存在,请求出m的取值;若不存在,请说明理由。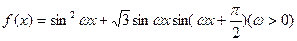
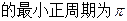 (1)求
(1)求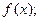
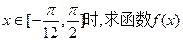 的值域。
的值域。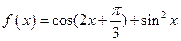 。
。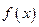 的最小正周期,并判断奇偶性;
的最小正周期,并判断奇偶性;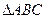 的三个内角,若
的三个内角,若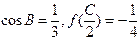 ,且C为锐角,求
,且C为锐角,求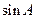 。
。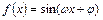 (
(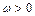 ,
,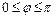 )为偶函数,且其图像上相邻的一个最高点和最低点之间距离为
)为偶函数,且其图像上相邻的一个最高点和最低点之间距离为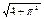 .
.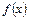 的解析式;
的解析式;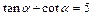 ,求
,求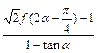 的值。
的值。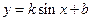 的最大值为
的最大值为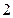 ,最小值为
,最小值为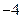 ,求
,求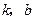 的值.
的值.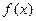 是定义在(0,3)上的函数,
是定义在(0,3)上的函数,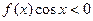 的解集是( )
的解集是( )
 )∪(
)∪(