题目内容
正三角形 的边长为2,将它沿高
的边长为2,将它沿高 翻折,使点
翻折,使点 与点
与点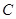 间的距离为1,此时二面角
间的距离为1,此时二面角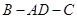 大小为 .
大小为 .
 的边长为2,将它沿高
的边长为2,将它沿高 翻折,使点
翻折,使点 与点
与点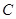 间的距离为1,此时二面角
间的距离为1,此时二面角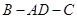 大小为 .
大小为 .600
试题分析:如下图所示,依题意知,
 是正三角形
是正三角形 的高,所以
的高,所以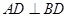 、
、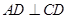 ,故
,故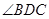 为二面角
为二面角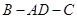 的平面角.又
的平面角.又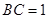 ,正三角形
,正三角形 的边长为2,则易知
的边长为2,则易知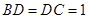 .即
.即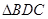 为正三角形,所以
为正三角形,所以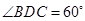 .即二面角
.即二面角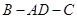 大小为
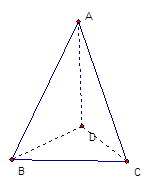
大小为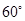 .
.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
题目内容
 的边长为2,将它沿高
的边长为2,将它沿高 翻折,使点
翻折,使点 与点
与点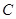 间的距离为1,此时二面角
间的距离为1,此时二面角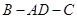 大小为 .
大小为 . 是正三角形
是正三角形 的高,所以
的高,所以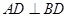 、
、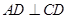 ,故
,故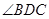 为二面角
为二面角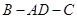 的平面角.又
的平面角.又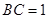 ,正三角形
,正三角形 的边长为2,则易知
的边长为2,则易知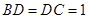 .即
.即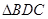 为正三角形,所以
为正三角形,所以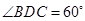 .即二面角
.即二面角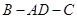 大小为
大小为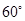 .
.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案