题目内容
设数列{an}的前n项和为Sn,对一切n∈N*,点(n,Sn)在函数f(x)=x2+x的图象上.
(1)求an的表达式;
(2)设![]() 使得不等式
使得不等式
![]() 都成立?若存在,求出a的取值范围;若不存在,请说明理由;
都成立?若存在,求出a的取值范围;若不存在,请说明理由;
(3)将数列{an}依次按1项,2项循环地分为(a1),(a2,a3),(a4),(a7),(a8,a9),(a10),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为{bn},求b100的值;
(4)如果将数列{an}依次按1项,2项,3项,…,m(m≥3)项循环;分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为{bn},提出同(3)类似的问题((3)应当作为特例),并进行研究,你能得到什么样的结论?
答案:
解析:
解析:
|
解:(1) 要使不等式 (3)数列{an}依次按1项,2项循环地分为(2),(4,6),(8),(10,12);(14),(16,18);(20),…,每一次循环记为一组.由于每一个循环含有2个括号,故b100是第50组中第2个括号内各数之和. 由分组规律知, 的等差数列 13分 所以 (4)当n是m的整数倍时,求bn的值. 数列{an}依次按1项、2项、3项,…,m项循环地分为(2),(4,6),(8,10,12),…, 则第m组、第2m组,…,第km组,…的各数之和也组成一个等差数列,其公差为m2(m+1) 17分 第m组的m个数之和为 当 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
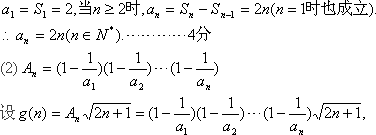
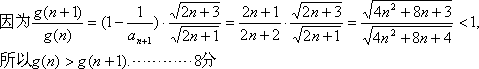 故
故