题目内容
已知向量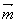 =(
=(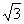 sin2x+2,cosx),
sin2x+2,cosx),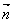 =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)= 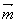 ·
·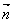 .
.
(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若A=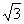 ,b=f(
,b=f(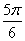 ),ΔABC的面积为
),ΔABC的面积为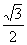 ,求a的值
,求a的值
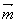 =(
=(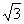 sin2x+2,cosx),
sin2x+2,cosx),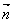 =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)= 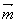 ·
·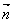 .
.(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若A=
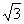 ,b=f(
,b=f(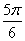 ),ΔABC的面积为
),ΔABC的面积为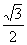 ,求a的值
,求a的值(1)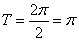
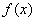 的单调递增区间为
的单调递增区间为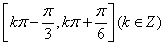
(2)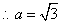
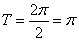
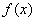 的单调递增区间为
的单调递增区间为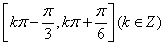
(2)
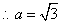
试题分析:解:(Ⅰ)
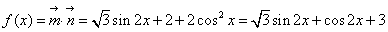
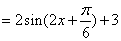 3分
3分∴
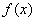 的最小正周期
的最小正周期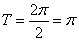 4分
4分由
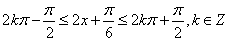 得
得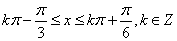
∴
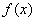 的单调递增区间为
的单调递增区间为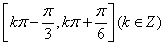 6分
6分(Ⅱ)
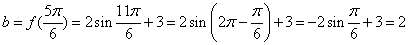 8分
8分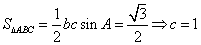 10分
10分在
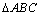 中,由余弦定理得
中,由余弦定理得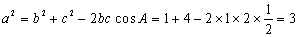
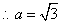 12分
12分点评:主要是考查了结合向量的数量积公式来化简三角函数关系式,然后借助于三角函数的性质来得到求解,属于基础题。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 的图象,只需把函数
的图象,只需把函数 的图象( )
的图象( ) 个长度单位
个长度单位 个长度单位
个长度单位 个长度单位
个长度单位 (其中
(其中 >0),且函数
>0),且函数 的最小正周期为
的最小正周期为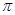 .
. 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.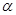 为锐角,且
为锐角,且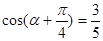 ,则
,则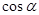 =_________.
=_________.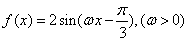 的图象向左平移
的图象向左平移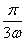 个单位得到函数
个单位得到函数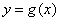 的图象,若
的图象,若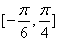 上为增函数,则
上为增函数,则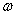 最大值为 .
最大值为 .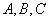 是△
是△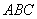 的三个内角,向量
的三个内角,向量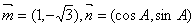 ,且
,且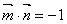
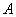 ;
;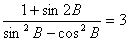 ,求
,求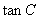 的值。
的值。 的图象,只需将函数
的图象,只需将函数 的图像
的图像 个长度单位
个长度单位 个长度单位
个长度单位 -2x)的单调递增区间是 ( )
-2x)的单调递增区间是 ( ) +
+ ,kπ+
,kπ+
