题目内容
已知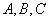 是△
是△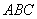 的三个内角,向量
的三个内角,向量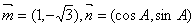 ,且
,且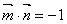
(1)求角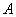 ;
;
(2)若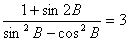 ,求
,求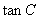 的值。
的值。
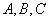 是△
是△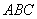 的三个内角,向量
的三个内角,向量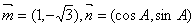 ,且
,且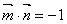
(1)求角
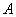 ;
;(2)若
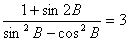 ,求
,求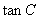 的值。
的值。(1) ;
;
(2)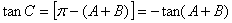
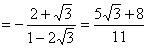 .
.
 ;
;(2)
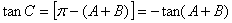
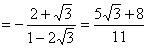 .
.试题分析:(1)
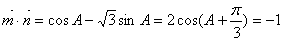 ,
,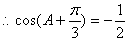 2分
2分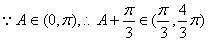 ,
,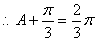 ,
, 6分
6分(2)
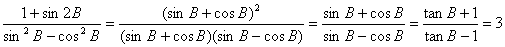
得
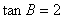 8分
8分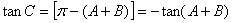
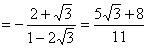 12分
12分点评:典型题,属于常见题型,通过计算平面向量的数量积,得到三角形边角关系,利用和差倍半的三角函数公式进一步转化。三角形中的问题,要注意角的范围。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

 在区间
在区间 上单调递减,且函数值从1减小到
上单调递减,且函数值从1减小到 ,那么此函数图象与
,那么此函数图象与 轴交点的纵坐标为( )
轴交点的纵坐标为( )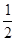



 的部分图象如图
的部分图象如图
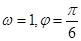



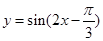 的图象,可以将函数
的图象,可以将函数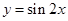 的图象( )
的图象( )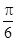 个长度单位
个长度单位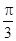 个长度单位
个长度单位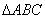 中,
中,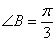 .
.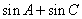 的取值范围;
的取值范围;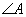 为锐角,求
为锐角,求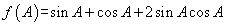 的最大值并求出此时角
的最大值并求出此时角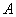 的大小.
的大小.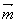 =(
=(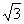 sin2x+2,cosx),
sin2x+2,cosx),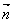 =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)= 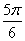 ),ΔABC的面积为
),ΔABC的面积为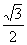 ,求a的值
,求a的值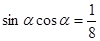 ,且
,且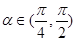 ,则
,则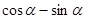 的值是
的值是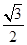
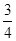
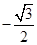
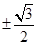
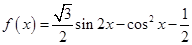 .
.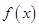 的最小值和最小正周期;
的最小值和最小正周期; 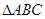 的内角
的内角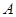 ,
,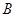 ,
,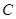 的对边分别为
的对边分别为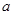 ,
,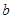 ,
,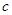 ,且
,且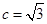 ,
,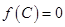 ,若
,若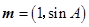 与
与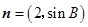 共线,求
共线,求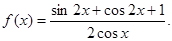
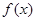 的定义域和值域;
的定义域和值域;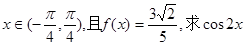 的值;
的值;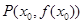
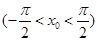 处的切线平行直线
处的切线平行直线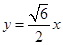 ,求
,求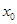 的值.
的值.