题目内容
设a、b、c分别是△ABC中∠A、∠B、∠C的对边,其外接圆半径为1,且(sinB+sinC+sinA)(sinB+sinC-sinA)=3sinBsinC,b、c是方程x2-3x+4cosA=0的两根(b>c).(1)求角A的度数及a、b、c的值;
(2)判定△ABC的形状,并求其内切圆的半径.
解:(1)由韦达定理b+c=3,b·c=4cosA,由正弦定理b=2RsinB=2sinB,c=2sinC.
∴2(sinB+sinC)=3,sinB·sinC=cosA.
∵(sinB+sinC+sinA)(sinB+sinC-sinA)=3sinBsinC,
利用平方差公式展开为(sinB+sinC)2-sin2A=3sinBsinC,
把sinB+sinC=![]() ,sinB·sinC=cosA代入上式可得
,sinB·sinC=cosA代入上式可得![]() -sin2A=3cosA.
-sin2A=3cosA.
整理得4cos2A-12cosA+5=0,
即(2cosA-5)(2cosA-1)=0,
∴cosA=![]() ,cosA=
,cosA=![]() (舍去).
(舍去).
∴∠A=60°.∴![]()
∵b>c,∴b=2,c=1.
由余弦定理a2=b2+c2-2bccosA=22+12-2×2×1×![]() =3,∴a=
=3,∴a=![]() .
.
(2)∵b2=a2+c2(由勾股定理).
∴△ABC是直角三角形.
如图所示,设内切圆半径是r,则∠OAB=30°,
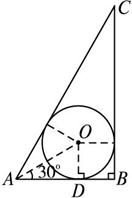
在△OAD中,AD=rcot30°=![]() r,∴
r,∴![]() r+r=1.∴内切圆半径r=
r+r=1.∴内切圆半径r=![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设a、b、c分别是方程2x=log
x,(
)x=log
x,(
)x=log2x的实数根,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、c<b<a |
| B、a<b<c |
| C、b<a<c |
| D、c<a<b |
设a、b、c分别是函数f(x)=(
)x-log2x,g(x)=2x-log
x,h(x)=(
)x-log
x的零点,则a、b、c的大小关系为( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、b<c<a |
| B、a<b<c |
| C、b<a<c |
| D、c<b<a |