Question

【题目】已知函数

(1)求证：函数f(x)-g(x)必有零点；

(2)设函数G(x)=f(x)-g(x)-1

①若函数G(x)有两相异零点且在上是减函数，求实数m的取值范围。

②是否存在整数a,b使得的解集恰好为若存在，求出a,b的值，若不存在，请说明理由。

Answer 1

【答案】（1）详见解析；（2）①（﹣∞，0]∪[2，+∞）；②或.

【解析】

（1）判断对应方程的△与0的关系，易得结论；

（2）由函数f（x）＝mx+3，g（x）＝x2+2x+m，我们易给出函数G（x）＝f（x）﹣g（x）﹣1，①若|G（x）|在[﹣1，0]上是减函数，根据对折变换函数图象的特征，我们分△≤0和△＞0两种情况进行讨论，可得到满足条件的m的取值范围；②若a≤G（x）≤b的解集恰好是[a，b]，则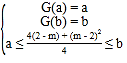将a，b代入消去m，可以求出a，b的值．

证明：（1）f（x）﹣g（x）＝﹣x2+（m﹣2）x+3﹣m．

令f（x）﹣g（x）＝0．

则△＝（m﹣2）2﹣4（m﹣3）＝m2﹣8m+16＝（m﹣4）2≥0恒成立．

所以方程f（x）﹣g（x）＝0有解．

所以函数f（x）﹣g（x）必有零点．

（2）①G（x）＝f（x）﹣g（x）﹣1＝﹣x2+（m﹣2）x+2﹣m．

①令G（x）＝0，△＝（m﹣2）2﹣4（m﹣2）＝（m﹣2）（m﹣6）．

当△≤0，即2≤m≤6时，G（x）＝﹣x2+（m﹣2）x+2﹣m≤0恒成立，

所以|G（x）|＝x2﹣（m﹣2）x+m﹣2．

因为|G（x）|在[﹣1，0]上是减函数，所以0．解得m≥2．

所以2≤m≤6．

当△＞0，即m＜2或m＞6时，|G（x）|＝|x2﹣（m﹣2）x+m﹣2|．

因为|G（x）|在[﹣1，0]上是减函数，

所以方程x2﹣（m﹣2）x+m﹣2＝0的两根均大于零或一根大于零另一根小于零

且x1．

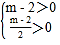所以或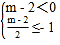

解得m＞2或m≤0．

所以m≤0或m＞6．

综上可得，实数m的取值范围为（﹣∞，0]∪[2，+∞）．

②因为a≤G（x）≤b的解集恰好是[a，b]，

所以

由

消去m，得ab﹣2a﹣b＝0，显然b≠2．

所以a1．

因为a，b均为整数，所以b﹣2＝±1或b﹣2＝±2．

解得或或或因为a＜b，且ab

所以或