题目内容
函数f(x)是定义在[0,1]上,满足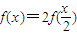 且f(1)=1,在每个区间
且f(1)=1,在每个区间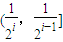 (i=1,2,3,…)上,y=f(x)的图象都是平行于x轴的直线的一部分.
(i=1,2,3,…)上,y=f(x)的图象都是平行于x轴的直线的一部分.(1)求f(0)及
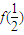 ,
,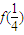 的值,并归纳出
的值,并归纳出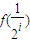 (i=1,2,3,…)的表达式;
(i=1,2,3,…)的表达式;(2)设直线
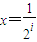 ,
,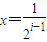 ,x轴及y=f(x)的图象围成的矩形的面积为ai(i=1,2,3,…),求a1,a2及
,x轴及y=f(x)的图象围成的矩形的面积为ai(i=1,2,3,…),求a1,a2及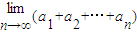 的值.
的值.
【答案】分析:(1)令式中的x=0,代入可得f(0),再令x=1,可得f( ),令x=
),令x= 可得f(
可得f( ),归纳可得;
),归纳可得;
(2)由题意可得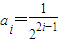 ,由等比数列的求和公式可求和,取极限即可.
,由等比数列的求和公式可求和,取极限即可.
解答:解:(1)由题意可得f(0)=2f(0),故f(0)=0,
同理可得f(1)=2f( ),解得
),解得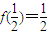 ,
,
所以f( )=2f(
)=2f( ),故
),故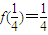 ,
,
由此可归纳出: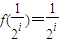 (i=1,2,3,…)
(i=1,2,3,…)
(2)当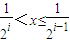 时,取
时,取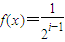 ,
,
∴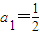 ,
,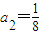 ,
,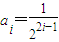 (i=1,2,3,…)
(i=1,2,3,…)
所以{an}是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
∴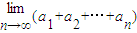 =
=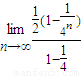 =
=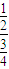 =
=
点评:本题考查归纳推理,以及数列的极限,属基础题.
 ),令x=
),令x= 可得f(
可得f( ),归纳可得;
),归纳可得;(2)由题意可得
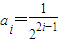 ,由等比数列的求和公式可求和,取极限即可.
,由等比数列的求和公式可求和,取极限即可.解答:解:(1)由题意可得f(0)=2f(0),故f(0)=0,
同理可得f(1)=2f(
 ),解得
),解得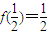 ,
,所以f(
 )=2f(
)=2f( ),故
),故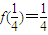 ,
,由此可归纳出:
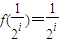 (i=1,2,3,…)
(i=1,2,3,…)(2)当
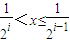 时,取
时,取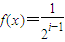 ,
,∴
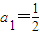 ,
,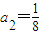 ,
,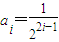 (i=1,2,3,…)
(i=1,2,3,…)所以{an}是首项为
 ,公比为
,公比为 的等比数列,
的等比数列,∴
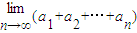 =
=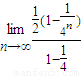 =
=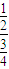 =
=
点评:本题考查归纳推理,以及数列的极限,属基础题.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,其最小正周期为3,且x∈(-
,0)时,f(x)=log2(-3x+1),则f(2011)=( )
| 3 |
| 2 |
| A、-2 |
| B、2 |
| C、4 |
| D、log27 |