题目内容
【题目】设集合![]() .如果对于
.如果对于![]() 的每一个含有
的每一个含有![]() 个元素的子集
个元素的子集![]() ,
, ![]() 中必有4个元素的和等于
中必有4个元素的和等于![]() ,称正整数
,称正整数![]() 为集合
为集合![]() 的一个“相关数”.
的一个“相关数”.
(Ⅰ)当![]() 时,判断5和6是否为集合
时,判断5和6是否为集合![]() 的“相关数”,说明理由;
的“相关数”,说明理由;
(Ⅱ)若![]() 为集合
为集合![]() 的“相关数”,证明:
的“相关数”,证明: ![]() ;
;
(Ⅲ)给定正整数![]() .求集合
.求集合![]() 的“相关数”
的“相关数” ![]() 的最小值.
的最小值.
【答案】(1)![]() 不是,
不是, ![]() 是(2)见解析(3)
是(2)见解析(3) ![]()
【解析】试题分析:(Ⅰ)由![]() 可得
可得![]() 及
及![]() ,对于
,对于![]() 个元素的子集可以举出反例
个元素的子集可以举出反例![]() 可证含有
可证含有![]() 个元素的子集只有
个元素的子集只有![]() ,满足题意;(Ⅱ)首先考察集合
,满足题意;(Ⅱ)首先考察集合![]() 的含有
的含有![]() 个元素的子集
个元素的子集![]() ,证明当
,证明当![]() 时,
时, ![]() 一定不是集合
一定不是集合![]() 的“相关数”,可得结果;(Ⅲ)先将集合
的“相关数”,可得结果;(Ⅲ)先将集合![]() 的元素分成如下
的元素分成如下![]() 组:
组: ![]() ,再将集合
,再将集合![]() 的元素剔除
的元素剔除![]() 和
和![]() 后,分成如下
后,分成如下![]() 组:
组: ![]() ,可得两者中同属对于
,可得两者中同属对于![]() 的一个含有
的一个含有![]() 个元素的子集
个元素的子集![]() 中至少一组无相同元素,可得结果.
中至少一组无相同元素,可得结果.
试题解析:(Ⅰ)当![]() 时,
时, ![]() ,
, ![]() .①对于
.①对于![]() 的含有
的含有![]() 个元素的子集
个元素的子集![]() ,因为
,因为![]() ,所以
,所以![]() 不是集合
不是集合![]() 的“相关数”.
的“相关数”.
②![]() 的含有
的含有![]() 个元素的子集只有
个元素的子集只有![]() ,因为
,因为![]() ,
,
所以![]() 是集合
是集合![]() 的“相关数”.
的“相关数”.
(Ⅱ)考察集合![]() 的含有
的含有![]() 个元素的子集
个元素的子集![]() .
.
![]() 中任意
中任意![]() 个元素之和一定不小于
个元素之和一定不小于![]() .
.
所以![]() 一定不是集合
一定不是集合![]() 的“相关数”.
的“相关数”.
所以当![]() 时,
时, ![]() 一定不是集合
一定不是集合![]() 的“相关数”.
的“相关数”.
因此若![]() 为集合
为集合![]() 的“相关数”,必有
的“相关数”,必有![]() .
.
即若![]() 为集合
为集合![]() 的“相关数”,必有
的“相关数”,必有![]() .
.
(Ⅲ)由(Ⅱ)得 ![]() .先将集合
.先将集合![]() 的元素分成如下
的元素分成如下![]() 组:
组:
![]() .对
.对![]() 的任意一个含有
的任意一个含有![]() 个元素的子集
个元素的子集![]() ,必有三组
,必有三组![]() 同属于集合
同属于集合![]() .再将集合
.再将集合![]() 的元素剔除
的元素剔除![]() 和
和![]() 后,分成如下
后,分成如下![]() 组:
组:
![]() .对于
.对于![]() 的任意一个含有
的任意一个含有![]() 个元素的子集
个元素的子集![]() ,必有一组
,必有一组![]() 属于集合
属于集合![]() .这一组
.这一组![]() 与上述三组
与上述三组![]() 中至少一组无相同元素,
中至少一组无相同元素,
不妨设![]() 与
与![]() 无相同元素.此时这
无相同元素.此时这![]() 个元素之和为
个元素之和为![]() .所以集合
.所以集合![]() 的“相关数”
的“相关数”![]() 的最小值为
的最小值为![]() .
.

【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).

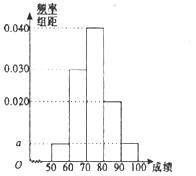
(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式: 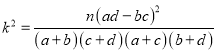 ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |