题目内容
定义在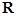 上的偶函数
上的偶函数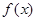 ,对任意实数
,对任意实数 都有
都有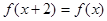 ,当
,当 时,
时,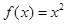 ,若在区间
,若在区间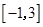 内,函数
内,函数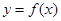 与函数
与函数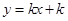 的图象恰有4个交点,则实数
的图象恰有4个交点,则实数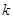 的取值范围是__________.
的取值范围是__________.
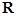 上的偶函数
上的偶函数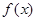 ,对任意实数
,对任意实数 都有
都有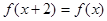 ,当
,当 时,
时,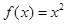 ,若在区间
,若在区间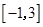 内,函数
内,函数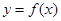 与函数
与函数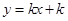 的图象恰有4个交点,则实数
的图象恰有4个交点,则实数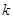 的取值范围是__________.
的取值范围是__________. 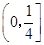
试题分析:因为,偶函数
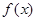 ,对任意实数
,对任意实数 都有
都有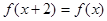 ,当
,当 时,
时,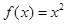 ,所以,在区间
,所以,在区间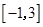 函数的图象为:
函数的图象为: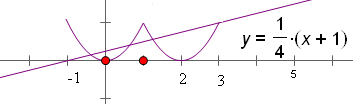
直线
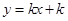 过(-1,0),所以函数
过(-1,0),所以函数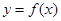 与函数
与函数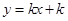 的图象恰有4个交点,则实数
的图象恰有4个交点,则实数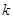 的取值范围是
的取值范围是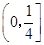 。
。点评:简单题,解答本题的关键是利用函数的奇偶性、周期性,准确地画出函数的图象,理解k的意义,利用数形结合思想解题。

练习册系列答案
相关题目
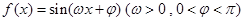 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表: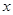
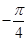

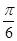
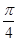
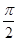
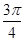
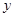
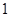
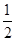
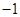
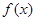 的解析式;
的解析式;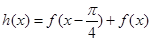 ,
,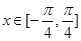 ,求
,求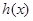 的最大值和最小值.
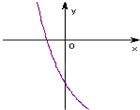
的最大值和最小值.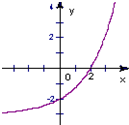 (2)
(2)

 在
在 上的单调;
上的单调; 上的值域是
上的值域是 的值.
的值.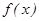 的定义域为D,若存在闭区间[a,b]
的定义域为D,若存在闭区间[a,b]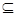 D,使得函数
D,使得函数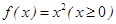 ;②
;②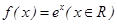 ;③
;③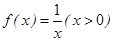 ;④
;④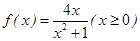 .
. g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.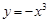
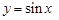
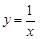
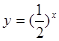
 的值域为[0,+
的值域为[0,+ ),则
),则 的最小
的最小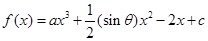 的图象过点
的图象过点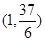 ,且在
,且在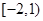 内单调递减,在
内单调递减,在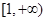 上单调递增。
上单调递增。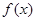 的解析式;
的解析式;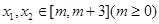 ,不等式
,不等式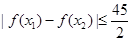 恒成立,试问这样的
恒成立,试问这样的 是否存在.若存在,请求出
是否存在.若存在,请求出