题目内容
18.已知f(x)=-x2-2x+1,x∈[-4,2],求f(x)的值域.分析 先求出函数f(x)的对称轴,再根据抛物线的开口向下知道:函数值随着点到对称轴距离增大而减小,求出最大值和最小值,由此求出值域
解答 解:因为函数f(x)=-x2-2x+1,所以对称轴方程是$x=-\frac{-2}{2(-1)}=-1$∈[-4,2],定义域关于对称轴对称,
因为抛物线的开口向下,所以:f(x)max=f(-1)=2,f(x)min=f(-4)=f(2)=-7,
由此可知:函数f(x)的值域是[-7,2].
点评 本题考查二次函数在闭区间上的值域,通过数形结合,可以看出最大值和最小值.由于函数和区间都是确定的,所以难度不大,属于基础题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
6.已知递增数列{an}的通项公式是an=n2+kn+4,则实数k的取值范围是( )
| A. | (-2,+∞) | B. | (-3,+∞) | C. | (-3,-2) | D. | (-∞,-3) |
6.若0<α<2π,cosα>$\frac{\sqrt{3}}{2}$,sinα<$\frac{1}{2}$,则角α的取值范围是( )
| A. | (-$\frac{π}{6}$,$\frac{π}{6}$) | B. | (0,$\frac{π}{6}$) | C. | (0,$\frac{π}{6}$)∪($\frac{5π}{3}$,2π) | D. | (0,$\frac{π}{6}$)∪($\frac{11π}{6}$,2π) |
3.在△ABC中,若sinA=cosB=$\frac{1}{2}$,则∠C=( )
| A. | 45° | B. | 60° | C. | 30° | D. | 90° |
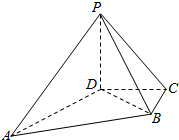 如图,在四棱锥P-ABCD中,PD=4,DC=DB=3,PB=PC=5,AD⊥DB.
如图,在四棱锥P-ABCD中,PD=4,DC=DB=3,PB=PC=5,AD⊥DB.