题目内容
6.若0<α<2π,cosα>$\frac{\sqrt{3}}{2}$,sinα<$\frac{1}{2}$,则角α的取值范围是( )| A. | (-$\frac{π}{6}$,$\frac{π}{6}$) | B. | (0,$\frac{π}{6}$) | C. | (0,$\frac{π}{6}$)∪($\frac{5π}{3}$,2π) | D. | (0,$\frac{π}{6}$)∪($\frac{11π}{6}$,2π) |
分析 由题意画出cosα=$\frac{\sqrt{3}}{2}$、sinα=$\frac{1}{2}$的三角函数线,由图形解答.
解答 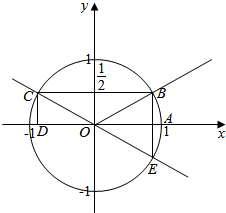 解:如图∠AOB的正弦弦为AB=$\frac{1}{2}$,余弦线为OA=$\frac{\sqrt{3}}{2}$,
解:如图∠AOB的正弦弦为AB=$\frac{1}{2}$,余弦线为OA=$\frac{\sqrt{3}}{2}$,
所以当0<α<2π,cosα>$\frac{\sqrt{3}}{2}$,sinα<$\frac{1}{2}$,则角α的取值范围是(0,$\frac{π}{6}$)∪($\frac{11π}{6}$,2π);
故选:D.
点评 本题考查了数形结合求角度范围;本题利用了三角函数线,关键是正确画出函数值为 $\frac{1}{2}$,$\frac{\sqrt{3}}{2}$的三角函数线.

练习册系列答案
相关题目
1.已知Z1,Z2,Z3∈C,下列结论正确的是( )
| A. | 若Z21+Z22+Z23=0,则Z1=Z2=Z3=0 | B. | 若Z21+Z22+Z23>0,则Z21+Z22>-Z23 | ||
| C. | 若Z21+Z22>-Z23,则Z21+Z22+Z23>0 | D. | 若$\overline{{Z}_{1}}$=-Z1,则Z1为纯虚数 |
11.设a,b,c∈R,则下列正确的是( )
| A. | 若ac>bc,则a>b | B. | 若a2>b2,则a>b | C. | 若$\sqrt{a}$<$\sqrt{b}$,则a<b | D. | 若$\frac{1}{a}$>$\frac{1}{b}$,则a<b |
15.已知全集I={0,1,2},A={1},B⊆I且满足A∩B={1}的B共有个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.淮北市文明创建活动正在轰轰烈烈的开展,第三方评估机构拟了解我市中小学生“社会主义核心价值观”掌握情况,已知不同学段学生掌握情况有差异,现从中小学生中抽取部分学生进行调查,在下面的抽样方法中,最合理的抽样方法是( )
| A. | 简单随机抽样 | B. | 按性别分层抽样 | C. | 按学段分层抽样 | D. | 系统抽样 |