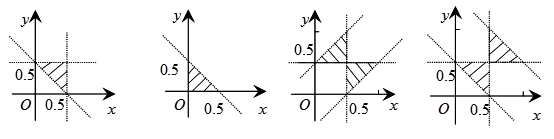
题目内容
定义: .在区域
.在区域 内任取一点
内任取一点 ,则
,则 、
、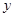 满足
满足 的概率为
的概率为
A. | B.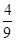 | C. | D.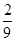 |
B
解析试题分析:根据定义可知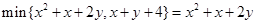 说明
说明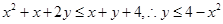 ,画出
,画出 表示的区域可知该区域是一个矩形,且面积为12,而
表示的区域可知该区域是一个矩形,且面积为12,而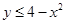 表示的是一条开口向下的抛物线的下半部分,它在矩形内的部分的面积为
表示的是一条开口向下的抛物线的下半部分,它在矩形内的部分的面积为 ,所以所求概率为
,所以所求概率为
考点:本小题主要考查新定义的转化和几何概型.
点评:本小题是与面积有关的几何概型的求解,解决本小题的关键是正确转化已知条件,将新定义问题向熟悉的数学问题转化,在解题时要注意转化思想的灵活应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
设变量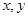 满足约束条件
满足约束条件 则
则 的最大值为
的最大值为
| A.0 | B.2 | C.4 | D.6 |
若变量 满足约束条件
满足约束条件 则
则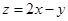 的最小值为
的最小值为
| A.4 | B.1 | C.0 | D. |
已知点(-2,1)和点(1,1)在直线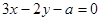 的两侧,则a的取值范围是( )
的两侧,则a的取值范围是( )
A. | B.(-1,8) |
| C.(-8,1) | D. |
已知实数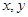 满足
满足 ,则目标函数
,则目标函数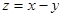 的最小值为
的最小值为
A.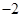 | B.5 | C.6 | D.7 |
若实数 满足
满足 则
则 的最小值是( )
的最小值是( )
| A.0 | B.1 | C. | D.9 |
不等式组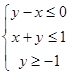 ,表示的平面区域的面积是( )
,表示的平面区域的面积是( )
A.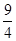 | B.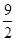 | C.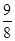 | D.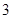 |
设x,y满足约束条件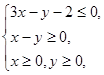 若目标函数
若目标函数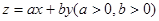 的最大值1,则
的最大值1,则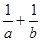 的最小值为
的最小值为
| A.4 | B.2 | C.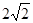 | D.1 |