题目内容
设x,y满足约束条件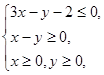 若目标函数
若目标函数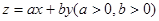 的最大值1,则
的最大值1,则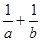 的最小值为
的最小值为
| A.4 | B.2 | C.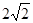 | D.1 |
A
解析试题分析:画出线性约束条件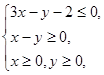 的可行域,由目标函数
的可行域,由目标函数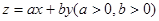 得,
得,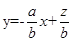 ,因为
,因为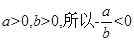 ,由
,由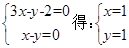 。所以目标函数过点(1,1)时,取最大值1,即
。所以目标函数过点(1,1)时,取最大值1,即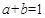 ,所以
,所以 。
。
考点:线性规划的有关知识。
点评:本题中给出a,b为正数使人较容易联想到基本不等式,但关键是基本不等式的灵活应用,此题我们通过1的代换把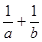 转化为
转化为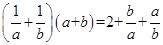 ,从而达到了应用基本不等式的条件。1的代换是这个地方常用的一中做题技巧,我们应熟练掌握。
,从而达到了应用基本不等式的条件。1的代换是这个地方常用的一中做题技巧,我们应熟练掌握。
对于解决线性规划的问题我们的关键点在于分析目标函数。目标函数除了我们常见的 这种形式外,还有常见的两种:
这种形式外,还有常见的两种: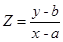 ,
,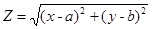 第一种的几何意义为:过点
第一种的几何意义为:过点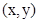 与点(a,b)直线的斜率。第二种的几何意义为:点
与点(a,b)直线的斜率。第二种的几何意义为:点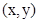 与点(a,b)的距离。
与点(a,b)的距离。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
定义: .在区域
.在区域 内任取一点
内任取一点 ,则
,则 、
、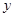 满足
满足 的概率为
的概率为
A. | B.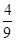 | C. | D.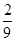 |
设变量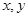 满足约束条件
满足约束条件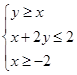 ,则
,则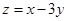 的最小值为( )
的最小值为( )
A.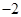 | B.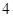 | C.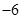 | D.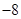 |
若实数x,y满足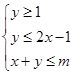 ,如果目标函数
,如果目标函数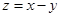 的最小值为
的最小值为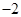 ,则实数m=( )
,则实数m=( )
| A. 8 | B. 0 | C. 4 | D.-8 |
设O为坐标原点,A(1,1),若点B(x,y)满足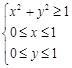 ,则
,则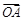 ·
·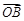 取得最小值时,点B的个数是
取得最小值时,点B的个数是
| A.1 | B.2 | C.3 | D.无数个 |
在平面直角坐标系中,已知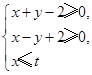 若目标函数
若目标函数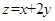 的最大值是10,则实数
的最大值是10,则实数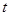 的值为
的值为
| A.1 | B.2 | C.3 | D.4 |
已知 是坐标原点,点
是坐标原点,点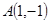 ,若点
,若点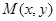 为平面区域
为平面区域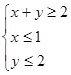 上的一个动点,
上的一个动点,
则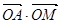 的取值范围是( )
的取值范围是( )
A.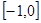 | B.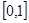 | C.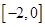 | D.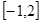 |
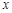 、
、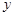 满足约束条件:
满足约束条件: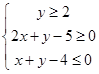 ,则
,则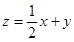 的最小值是
的最小值是
| A.2 | B.3 | C.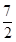 | D.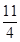 |
设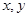 满足约束条件
满足约束条件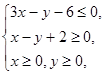 若目标函数
若目标函数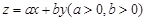 的值是最大值为12,则
的值是最大值为12,则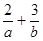 的最小值为( ).
的最小值为( ).
A.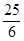 | B.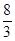 | C.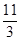 | D.4 |