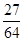题目内容
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
(1);(2);(3)见解析.
试题分析:(1)先记“甲以4比1获胜”为事件A,由题意甲乙一共比赛5局,则甲前4局比赛中有且只有3局获胜,第5局比赛一定获胜,易得甲以4比1获胜的概率为P(A)=
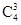 ()3·()4-3·=;(2)同(1)中道理,“乙获胜且比赛局数多于5局”分两种情况:一是比赛6局,二是比赛7局,分别计算出概率再相加即得结论;(3)比赛的局数的可能值为4、5、6、7,分别计算取不同值时的概率,列表得分布列.
()3·()4-3·=;(2)同(1)中道理,“乙获胜且比赛局数多于5局”分两种情况:一是比赛6局,二是比赛7局,分别计算出概率再相加即得结论;(3)比赛的局数的可能值为4、5、6、7,分别计算取不同值时的概率,列表得分布列.试题解析:(1)由已知,甲、乙两名运动员在每一局比赛中获胜的概率都是. 1分
记“甲以4比1获胜”为事件A,则P(A)=
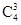 ()3·()4-3·=. 3分
()3·()4-3·=. 3分(2)记“乙获胜且比赛局数多于5局”为事件B.
因为乙以4比2获胜的概率为P1=
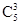
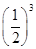 ·
·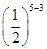 ·=,
·=,乙以4比3获胜的概率为P2=
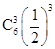 ·
·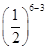 ·=,
·=,所以P(B)=P1+P2=. 7分
(3)设比赛的局数位X,则X的可能取值为4,5,6,7. 8分
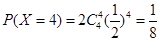 ,
,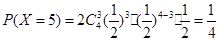 ,
,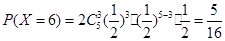 ,
,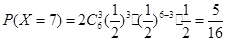 , 11分
, 11分比赛局数的分布列为
| X | 4 | 5 | 6 | 7 |
| P | 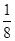 | 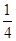 | 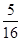 | 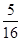 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求
 22℃
22℃ ℃
℃

 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.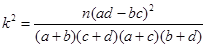



 则射击次数为3的概率为 ( ).
则射击次数为3的概率为 ( ).