题目内容
已知等差数列的前n项和为a,前2n项和为b,求前3n项和.
答案:
解析:
提示:
解析:
|
S3n=3(b-a). 由题设Sn=a,S2n=b,所以an+1+…+a2n=b-a,而(a1+…+an)+(a2n+1+…+a3n)=2(an+1+…+a2n),从而S3n=(a1+a2+…+an)+(an+1+…a2n)+(a2n+1+…a3n)=3(an+1+…a2n)=3(b-a). |
提示:
|
[提示]求解本题的一个基本方法是根据两个已知条件,列出关于首项a1和公差d的方程组,解出a1和d,然后代入S3n的表达式,但这种方法计算比较繁琐.换一个角度思考,运用等差数列的性质,不求a1和d,从整体上直接求出S3n的值. [说明]从本题的求解过程中,可以得到等差数列的又一个重要性质:“若{an}成等差数列,则a1+a2+…+ak,ak+1+ak+2+…+a2k,a2k+1+a2k+2+…+a3k,…也成等差数列”,运用这一性质求解类似的问题,可以收到化繁为简的效果. |

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且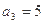 ,
,

 ,求数列
,求数列 的前n项和
的前n项和