题目内容
已知等差数列的前n项和为Sn,且Sp=Sq(p≠q,p、q∈N),则Sp+q=分析:利用
是关于n的一次函数,设Sp=Sq=m,
=x,则(
,p)、(
,q)、
(x,p+q)在同一直线上,由两点斜率相等解得x=0,求得答案.
| Sn |
| n |
| Sp+q |
| p+q |
| m |
| p |
| m |
| q |
(x,p+q)在同一直线上,由两点斜率相等解得x=0,求得答案.
解答:解:设Sp=Sq=m,
=x,则(
,p)、(
,q)、
(x,p+q)在同一直线上,
由两点斜率相等可知
=
解得x=0,
∵p+q≠0
∴Sp+q=0;
故答案为:0.
| Sp+q |
| p+q |
| m |
| p |
| m |
| q |
(x,p+q)在同一直线上,
由两点斜率相等可知
| q-p | ||||
|
| p+q-p | ||
x-
|
解得x=0,
∵p+q≠0
∴Sp+q=0;
故答案为:0.
点评:本题主要考查了等差数列的前n项的和.解题的关键是利用一次函数的性质,及数形结合的思想,转化和化归的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且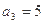 ,
,

 ,求数列
,求数列 的前n项和
的前n项和