题目内容
【题目】已知函数 
的最小正周期是 
，若将其图象向右平移 
个单位后得到的图象关于 
轴对称，则函数 
的图象（ ）
A.关于直线 
对称
B.关于直线 
对称
C.关于点 
对称
D.关于点 
对称
【答案】D
【解析】∵函数 
的最小正周期是 
，∴ 
，
将其图象向右平移 
个单位后得到的函数的表达式为 
，又 
的图象关于 
轴对称，
∴ 
，∴ 
, 
当 
时， 
，即 
易得： 
， 
,函数 
的图象关于点 
对称. 所以答案是：D
【考点精析】利用函数y=Asin（ωx+φ）的图象变换对题目进行判断即可得到答案，需要熟知图象上所有点向左（右）平移
个单位长度，得到函数
的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的
倍（纵坐标不变），得到函数
的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的
倍（横坐标不变），得到函数
的图象．
练习册系列答案
相关题目
【题目】（某保险公司有一款保险产品的历史户获益率（获益率=获益÷保费收入）的频率分布直方图如图所示：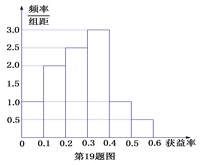
（Ⅰ）试估计平均收益率；
（Ⅱ）根据经验若每份保单的保费在 
元的基础上每增加 
元，对应的销量 
（万份）与 （元）有较强线性相关关系，从历史销售记录中抽样得到如下 
组 与 的对应数据：
|
|
|
|
|
|
销量 |
|
|
|
|
|
（ⅰ）根据数据计算出销量 （万份）与 （元）的回归方程为 
；
（ⅱ）若把回归方程 当作 与 的线性关系，用（Ⅰ）中求出的平均获益率估计此产品的获益率，每份保单的保费定为多少元时此产品可获得最大获益，并求出该最大获益.
参考公示： 
