题目内容
| |||||||||||||||
解析:
(1) |
P(0,b) M(a,0)没N(x,y)由 由 将②代入①得曲线C的轨迹方程为y2=4x 理科5分 文科6分 |
(2) |
点F′(-1,0),设直线l:y=k(x+1)代入y2=4x k2x2+2(k2-2)x+k2=0 由 设A(x1,y1) B(x2,y2) D(x0,y0) 则
故直线DE方程为 令y=0得 即 |
(3) |
设点Q的坐标为(-1,t),过点Q的切线为:y-t=k(x+1) 代入y2=4x消去x整理得ky2-4y+4t+4k=0 12分 △=16-16k(t+k)令 两切线l1,l2的斜率k1,k2是此方程的两根 ∴k1·k2=-1故l1⊥l2 14分 |

| |||||||||||
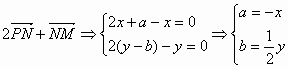 ②
②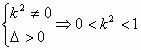 理科7分 文科8分
理科7分 文科8分