题目内容
已知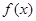 是定义在R上的偶函数,且以2为周期,则“
是定义在R上的偶函数,且以2为周期,则“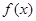 为[0,1]上的增函数”是“
为[0,1]上的增函数”是“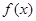 为[3,4]上的减函数”的( )
为[3,4]上的减函数”的( )
| A.既不充分也不必要的条件 | B.充分而不必要的条件 |
| C.必要而不充分的条件 | D.充要条件 |
D
解析试题分析:因为函数f(x) 是定义在R上的偶函数,则f(-x)=f(x),且以2为周期f(2+x)=f(x),则f(x) 为[0,1]上的增函数,则可知在[-1,0]上为减函数,在由x 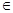 [3,4],可知x-4
[3,4],可知x-4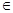 [-1,0],那么f(x-4)=f(x),故有f(x)为[3,4]上的减函数,并且条件和结论等价,因此选D.
[-1,0],那么f(x-4)=f(x),故有f(x)为[3,4]上的减函数,并且条件和结论等价,因此选D.
考点:本试题主要考查了函数的奇偶性和周期性的运用。
点评:解决该试题的关键是利用函数的周期性和单调性来确定在给定的区间的单调性。解决未知区间的单调性问题,将未知的变量转换到已知区间来判定这是一般的解题思路。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
命题“存在 ,使
,使 ”的否定是 ( )
”的否定是 ( )
A.存在 ,使 ,使 |
B.不存在 ,使 ,使 |
C.对于任意  ,都有 ,都有 |
D.对于任意 ,都有 ,都有 |
“直线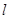 与平面a内无数条直线都平行”是“直线
与平面a内无数条直线都平行”是“直线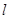 与平面a平行”的( )
与平面a平行”的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.不充分也不必要条件 |
已知 是直线,
是直线, 是平面,且
是平面,且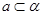 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题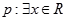 ,使
,使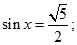 命题
命题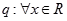 ,都有
,都有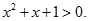
给出下列结论:① 命题“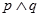 ”是真命题 ② 命题“
”是真命题 ② 命题“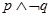 ”是假命题
”是假命题
③ 命题“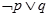 ”是真命题; ④ 命题“
”是真命题; ④ 命题“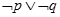 ”是假命题
”是假命题
其中正确的是
| A.② ④ | B.② ③ | C.③ ④ | D.① ② ③ |
设 ,
, 是定义在R上的函数,
是定义在R上的函数, ,则“
,则“ ,
, 均为偶函数”是“
均为偶函数”是“ 为偶函数”的( )
为偶函数”的( )
| A.充分而不必要的条件 | B.必要而不充分的条件 |
| C.充分必要条件 | D.既不充分也不必要的条件 |
设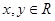 ,则“
,则“ 且
且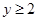 ”是“
”是“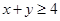 ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知
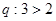 ,则下列判断中,错误的是( )
,则下列判断中,错误的是( )
| A.p或q为真,非q为假 | B.p或q为真,非p为假 |
| C.p且q为假,非p为真 | D.p且q为假,p或q为真 |
 ,定义运算
,定义运算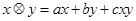 ,其中
,其中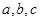 是常数,等式右边的运算是通常的加法和乘法运算.已知
是常数,等式右边的运算是通常的加法和乘法运算.已知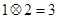 ,
, ,并且有一个非零常数
,并且有一个非零常数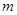 ,使得
,使得 ,都有
,都有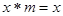 ,则
,则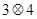 的值是( )
的值是( )