题目内容
（2013•天津）设函数f（x）=ex+x-2，g（x）=lnx+x2-3．若实数a，b满足f（a）=0，g（b）=0，则（ ）
分析：先判断函数f（x），g（x）在R上的单调性，再利用f（a）=0，g（b）=0判断a，b的取值范围即可．
解答：解：①由于y=ex及y=x-2关于x是单调递增函数，∴函数f（x）=ex+x-2在R上单调递增，
分别作出y=ex，y=2-x的图象，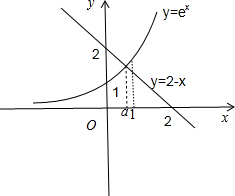
∵f（0）=1+0-2＜0，f（1）=e-1＞0，f（a）=0，∴0＜a＜1．
同理g（x）=lnx+x2-3在R+上单调递增，g（1）=ln1+1-3=-2＜0，g（
）=ln
+(
)2-3=
ln3＞0，g（b）=0，∴1＜b＜
．
∴g（a）=lna+a2-3＜g（1）=ln1+1-3=-2＜0，
f（b）=eb+b-2＞f（1）=e+1-2=e-1＞0．
∴g（a）＜0＜f（b）．
故选A．
分别作出y=ex，y=2-x的图象，
∵f（0）=1+0-2＜0，f（1）=e-1＞0，f（a）=0，∴0＜a＜1．同理g（x）=lnx+x2-3在R+上单调递增，g（1）=ln1+1-3=-2＜0，g（
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
∴g（a）=lna+a2-3＜g（1）=ln1+1-3=-2＜0，
f（b）=eb+b-2＞f（1）=e+1-2=e-1＞0．
∴g（a）＜0＜f（b）．
故选A．
点评：熟练掌握函数的单调性、函数零点的判定定理是解题的关键．
练习册系列答案
相关题目