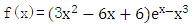题目内容
已知函数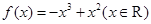 ,
, 满足
满足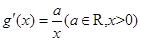 ,且
,且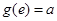 ,
, 为自然对数的底数.
为自然对数的底数.
(1)已知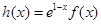 ,求
,求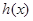 在
在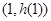 处的切线方程;
处的切线方程;
(2)若存在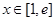 ,使得
,使得
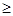
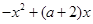 成立,求
成立,求 的取值范围;
的取值范围;
(3)设函数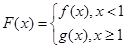 ,
, 为坐标原点,若对于
为坐标原点,若对于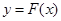 在
在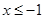 时的图象上的任一点
时的图象上的任一点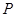 ,在曲线
,在曲线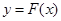
 上总存在一点
上总存在一点 ,使得
,使得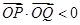 ,且
,且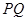 的中点在
的中点在 轴上,求
轴上,求 的取值范围.
的取值范围.
(1)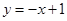 ;(2)
;(2)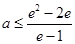 ;(3)
;(3)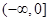 .
.
解析试题分析:(1)应用导数的几何意义,求导数,求斜率,确定切线方程;
(2)由已知确定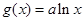 ;
;
根据
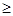
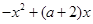 得:
得: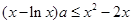 .
.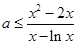 ,只需
,只需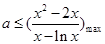 .
.
应用导数,求函数 ,
,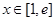 ,的最大值即得解;
,的最大值即得解;
(3)设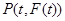 为
为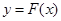 在
在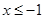 时的图象上的任意一点,可得
时的图象上的任意一点,可得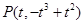 ,
,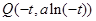 ,
, .
.
由于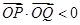 ,得到
,得到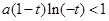 .
.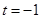 ,
, 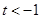 的情况,求得
的情况,求得 的取值范围.
的取值范围.
方法比较明确,分类讨论、转化与化归思想的应用,是解决问题的关键.
试题解析:(1)
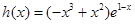 ,
,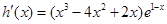
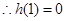 ,
,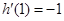

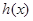 在
在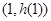 处的切线方程为:
处的切线方程为: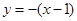 ,即
,即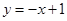 4分
4分
(2)
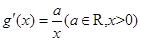 ,
,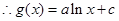
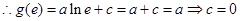 ,从而
,从而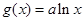 5分
5分
由
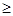
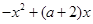 得:
得: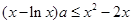 .
.
由于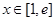 时,
时,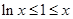 ,且等号不能同时成立,所以
,且等号不能同时成立,所以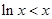 ,
,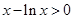 .
.
从而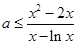 ,为满足题意,必须
,为满足题意,必须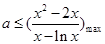 . 6分
. 6分
设 ,
,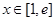 ,则
,则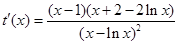 .
. 
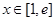 ,
,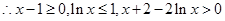 ,
,
从而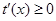 ,
,
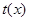 在
在 上为增函数,
上为增函数,
所以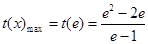 ,从而
,从而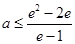 . 9分
. 9分
(3)设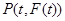 为
为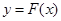 在
在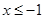 时的图象上的任意一点,则
时的图象上的任意一点,则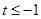

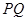 的中点
的中点

练习册系列答案
相关题目
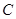 :
: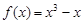
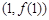 处的切线方程;
处的切线方程;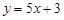 平行的曲线C的切线方程.
平行的曲线C的切线方程.
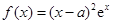 在
在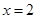 时取得极小值.
时取得极小值. 的值;
的值;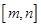 ,使得
,使得 在该区间上的值域为
在该区间上的值域为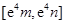 ?若存在,求出
?若存在,求出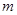 ,
,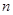 的值;
的值; R).
R).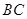 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)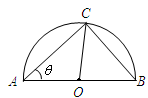
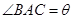 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为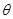 的函数
的函数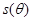 ;
;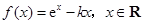
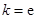 ,试确定函数
,试确定函数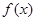 的单调区间;
的单调区间;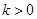 ,且对于任意
,且对于任意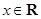 ,
,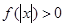 恒成立,试确定实数
恒成立,试确定实数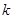 的取值范围;
的取值范围;