题目内容
7.空间四点A,B,C,D满足|$\overrightarrow{AB}$|=2,|$\overrightarrow{BC}$|=3,|$\overrightarrow{CD}$|=3$\sqrt{6}$,|$\overrightarrow{DA}$|=7.则$\overrightarrow{AC}$•$\overrightarrow{BD}$的值为0.分析 先把ABCD看成是平面图形,过B作BE垂直AC,过D作DF垂直AC,运用勾股定理,可得E,F重合,再将图形沿AC或BD折起,便是空间图形,运用线面垂直的判定和性质,可得AC⊥BD,再由向量数量积的性质,即可得到答案.
解答 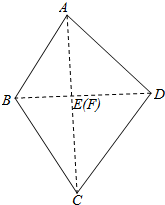 解:由|$\overrightarrow{AB}$|=2,|$\overrightarrow{BC}$|=3,|$\overrightarrow{CD}$|=3$\sqrt{6}$,|$\overrightarrow{DA}$|=7.
解:由|$\overrightarrow{AB}$|=2,|$\overrightarrow{BC}$|=3,|$\overrightarrow{CD}$|=3$\sqrt{6}$,|$\overrightarrow{DA}$|=7.
根据数据可知AB2+CD2=BC2+DA2=58,
BC2-AB2=CD2-DA2.
先把ABCD看成是平面图形,
过B作BE垂直AC,过D作DF垂直AC,
则AB2=AE2+BE2,BC2=CE2+BE2,
则BC2-AB2=CE2-AE2.
同理CD2-DA2=CF2-AF2,即CF2-AF2=CE2-AE2,
又因为A,E,F,C在一条直线上,
所以满足条件的只能是E,F重合,即有AC垂直BD,
再将图形沿AC或BD折起,便是空间图形,
由AC⊥BE,AC⊥DE,即有AC⊥平面BDE,则AC⊥BD,
即$\overrightarrow{AC}$•$\overrightarrow{BD}$=0.
故答案为:0.
点评 本题考查空间直线和平面的位置关系,以及向量的数量积的性质,考查空间想象能力,属于中档题.

练习册系列答案
相关题目
18.设等比数列{an}的前n项和为Sn,若a3=2a4=2,则S6等于( )
| A. | 31 | B. | $\frac{31}{2}$ | C. | $\frac{63}{4}$ | D. | $\frac{127}{8}$ |
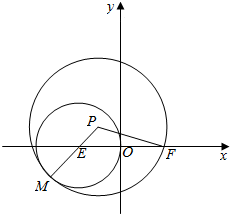 如图,圆E:(x+2)2+y2=4,点F(2,0),动圆P过点F,且与圆E内切于点M,求动圆P的圆心P的轨迹方程.
如图,圆E:(x+2)2+y2=4,点F(2,0),动圆P过点F,且与圆E内切于点M,求动圆P的圆心P的轨迹方程.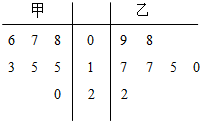 如图所示的茎叶图为甲、乙两家连锁店七天内销售额的某项指标统计:
如图所示的茎叶图为甲、乙两家连锁店七天内销售额的某项指标统计: