题目内容
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=| 3 |
| 2 |
| 1 |
| 2 |
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(Ⅱ)以该椭圆的长轴为直径作圆,判断点C与该圆的位置关系.
分析:(I)先以AB所在直线为x轴,AB中垂线为y轴建立直角坐标系,进而可知A,B的坐标,设椭圆的标准方程,根据AB的距离求得c,把x=c代入椭圆方程,求得
=
,进而根据a,b和c的关系求得a和b,则椭圆的方程可得.
(II)以该椭圆的长轴为直径作圆,求出点C到圆心的距离,与a比较即可判断点C与该圆的位置关系.
| b2 |
| a |
| 3 |
| 2 |
(II)以该椭圆的长轴为直径作圆,求出点C到圆心的距离,与a比较即可判断点C与该圆的位置关系.
解答: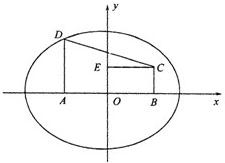 解:(Ⅰ)如图,以AB所在直线为x轴,
解:(Ⅰ)如图,以AB所在直线为x轴,
AB中垂线为y轴建立直角坐标系,⇒A(-1,0),B(1,0).
设椭圆方程为
+
=1.
令 x=c⇒y0=
,
∴
⇒
.
∴椭圆C的方程是:
+
=1;
(Ⅱ) 点C到原点的距离为:
|OC|=
=
< 2=a
∴点C在圆内.
 解:(Ⅰ)如图,以AB所在直线为x轴,
解:(Ⅰ)如图,以AB所在直线为x轴,AB中垂线为y轴建立直角坐标系,⇒A(-1,0),B(1,0).
设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
令 x=c⇒y0=
| b2 |
| a |
∴
|
|
∴椭圆C的方程是:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ) 点C到原点的距离为:
|OC|=
|
| ||
| 2 |
∴点C在圆内.
点评:本题主要考查了椭圆的标准方程和直线与椭圆的关系.考查了学生转化和化归的数学思想,基本的运算能力.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则