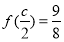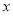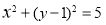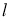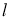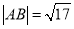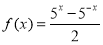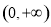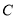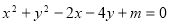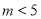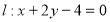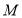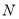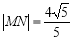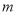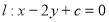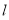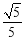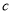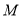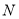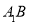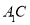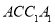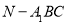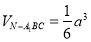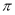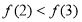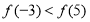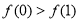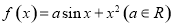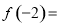题目内容
下列四个命题:
①方程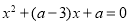 若有一个正实根,一个负实根,则
若有一个正实根,一个负实根,则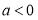 ;
;
②函数 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③函数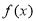 的值域是
的值域是 ,则函数
,则函数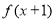 的值域为
的值域为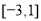 ;
;
④一条曲线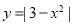 和直线
和直线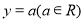 的公共点个数是
的公共点个数是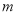 ,则
,则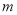 的值不可能是
的值不可能是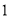 .
.
其中正确的有________________(写出所有正确命题的序号).
①④
【解析】
试题分析:若方程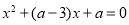 若有一个正实根
若有一个正实根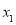 ,一个负实根
,一个负实根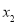 ,则满足
,则满足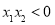 .由韦达定理可得
.由韦达定理可得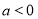 .所以①正确.因为函数
.所以①正确.因为函数 的定义域为
的定义域为 .解得
.解得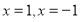 .所以函数图像为两个点,所以既是偶函数又是奇函数.所以②不正确.因为函数
.所以函数图像为两个点,所以既是偶函数又是奇函数.所以②不正确.因为函数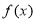 通过向左平移1个单位得到函数
通过向左平移1个单位得到函数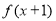 .所以值域没有改变.所以③不正确.由于曲线
.所以值域没有改变.所以③不正确.由于曲线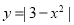 对应的函数是偶函数,直线
对应的函数是偶函数,直线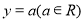 也是偶函数,所以根据偶函数的图像性质,只有一个交点是不成立的.所以④正确,综上①④正确,故填①④.
也是偶函数,所以根据偶函数的图像性质,只有一个交点是不成立的.所以④正确,综上①④正确,故填①④.
考点:1.二次函数的根的分布.2.函数的奇偶性.3.函数的最值问题.4.函数的图像的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目