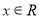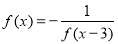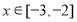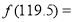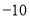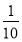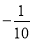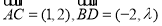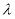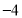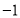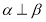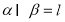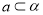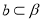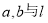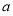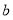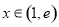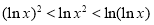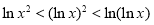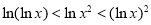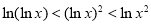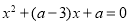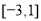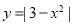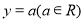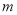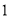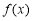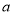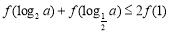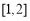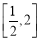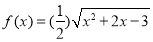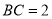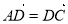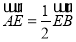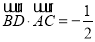题目内容
已知圆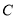 的方程:
的方程: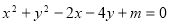 ,其中
,其中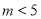 .
.
(1)若圆C与直线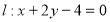 相交于
相交于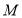 ,
,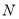 两点,且
两点,且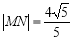 ,求
,求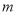 的值;
的值;
(2)在(1)条件下,是否存在直线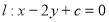 ,使得圆上有四点到直线
,使得圆上有四点到直线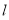 的距离为
的距离为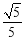 ,若存在,求出
,若存在,求出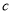 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
(1)4;(2)
【解析】
试题分析:(1)因为已知直线被圆截得的弦长,根据圆中的重要三角形,要表示出弦心距和圆的半径.通过将圆的一般方程化为标准方程可得圆心坐标和圆的半径,根据点到直线的距离公式,即可求得弦心距,从而求出m的值.
(2)由(1)可得圆的方程,半径为1,所以要存在直线 ,使得圆上有四点到直线
,使得圆上有四点到直线 的距离为
的距离为 .只需要圆心距小于
.只需要圆心距小于 即可,所以通过解不等式即可得c的范围.
即可,所以通过解不等式即可得c的范围.
试题解析:(1)圆的方程化为 ,圆心 C(1,2),半径
,圆心 C(1,2),半径  ,
,
则圆心C(1,2)到直线 的距离为
的距离为  3分
3分
由于 ,则
,则 ,有
,有 ,
,
 得
得 . 6分
. 6分
(2)假设存在直线 ,使得圆上有四点到直线
,使得圆上有四点到直线 的距离为
的距离为 , 7分
, 7分
由于圆心 C(1,2),半径 , 则圆心C(1,2)到直线
, 则圆心C(1,2)到直线 的距离为
的距离为
 , 10分
, 10分
解得 . 13分
. 13分
考点:1.直线与圆的位置关系.2.直线与圆的弦长公式.3.动态的思维.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目