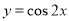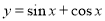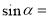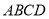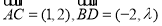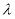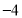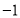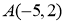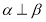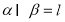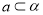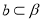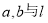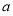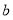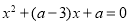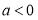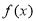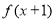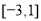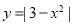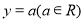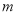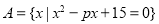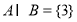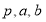题目内容
注:此题选A题考生做①②小题,选B题考生做①②③小题.
已知圆C: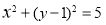 ,直线
,直线 .
.
①求证:对任意 ,直线
,直线 与圆C总有两个不同的交点;
与圆C总有两个不同的交点;
②当m=1时,直线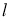 与圆C交于M、N两点,求弦长|MN|;
与圆C交于M、N两点,求弦长|MN|;
③设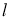 与圆C交于A、B两点,若
与圆C交于A、B两点,若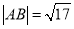 ,求
,求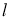 的倾斜角.
的倾斜角.
①见解析;② ;③
;③
【解析】
试题分析:①法一:证明用点到直线的距离恒小于圆的半径,(此法计算量较大,故通常不选用此方法)。法二:证直线恒过定点,且此顶点在圆内。②根据圆心和弦中点的连线垂直平分弦,应先求圆心到直线的距离再用勾股定理求弦长。③根据弦长可求圆心到直线的距离,即可求出直线的斜率,根据斜率可求得倾斜角。
试题解析:【解析】
①∵直线 恒过
恒过 点,又∵点
点,又∵点 在圆C:
在圆C:
 内,∴对
内,∴对 ,直线
,直线 与圆C总有两个不同的交点。(A:7分,B:5分)
与圆C总有两个不同的交点。(A:7分,B:5分)
②当m=1时,直线 ;圆心C(0,1)到直线
;圆心C(0,1)到直线 的距离等于
的距离等于 ,又∵圆C的半径为
,又∵圆C的半径为 ,∴弦长|MN|
,∴弦长|MN|  ;(A:14分,B:9分)
;(A:14分,B:9分)
③∵ ,∴
,∴ ,又∵圆C的半径为
,又∵圆C的半径为 ,∴圆心C(0,1)到直线
,∴圆心C(0,1)到直线 的距离等于
的距离等于 ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴直线
,∴直线 的倾斜角为
的倾斜角为 。(B:14分)
。(B:14分)
考点:直线过定点问题,点到直线的距离公式,圆的弦长。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目